mathématiques

Article principal

• MATHÉMATIQUES

  • Écrit par Encyclopædia Universalis
  • 2 médias
  

  Les mathématiques étudient les nombres ainsi que leurs relations entre eux et avec le monde réel. Elles sont souvent décrites comme une sorte de langage. On les utilise tous les jours, pour lire l’heure, jouer ou construire des objets. Types de mathématiques Les mathématiques comprennent plusieurs branches, dont l’arithmétique, l’algèbre, la géométrie, la trigonométrie, le calcul, les statistiques et les probabilités [...]

Articles associés

• ADDITION

  • Écrit par Alain MATTHÈS

  L’addition (du latin addere, « ajouter ») est l’une des 4 opérations élémentaires de l’arithmétique. Elle consiste à compter la réunion d’objets contenus dans des collections. Elle sert aussi à déterminer une grandeur obtenue par l’ajout de 2 grandeurs de même nature, comme les longueurs. Un enfant qui mesurait 147 centimètres et a grandi de 3 centimètres mesure ainsi 150 centimètres [...]

• AIRE

  • Écrit par Alain MATTHÈS

  En géométrie, l’aire (du latin area, qui signifie « surface plane ») désigne la mesure d’une surface. En géographie, le terme « superficie » lui est préféré. Dans la langue de tous les jours, si une « surface » peut être cultivée, c’est la « superficie » cultivée qui est exprimée en hectares. Les Égyptiens savaient déjà évaluer les aires des figures planes comme le triangle, le rectangle ou le trapèze [...]

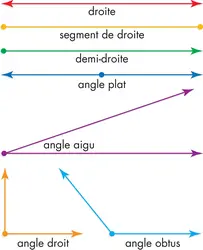
• ANGLE, géométrie

  • Écrit par Olivier GENIN

  Un angle est une portion de plan délimité par deux droites sécantes en un point. Ce point d’intersection est appelé sommet de l’angle. La notation d’un angle, où le point O est le sommet de l’angle et les demi-droites [OA) et [OB) les côtés de l’angle, est AOB. Angles opposés Deux angles sont opposés par le sommet s’ils ont le même sommet et si leurs côtés sont dans le prolongement l’un de l’autre [...]

• ARITHMÉTIQUE

  • Écrit par Encyclopædia Universalis

  L’arithmétique est la branche la plus élémentaire des mathématiques. C’est elle qui permet de compter et de réaliser les 4 opérations élémentaires (addition, soustraction, multiplication, division). Toutes les autres branches des mathématiques reposent sur ses principes et ses règles. Nous utilisons l’arithmétique tous les jours, pour faire un achat, mesurer une distance ou simplement pour compter [...]

• ARITHMÉTIQUES, livre de Diophante

  Diophante d'Alexandrie, un mathématicien grec du 3e siècle, parfois appelé le « père de l'algèbre », est connu par son ouvrage les Arithmétiques, qui traite des solutions des équations algébriques. On ne sait pratiquement rien de sa vie, et ses dates de naissance et de mort sont très controversées. Les Arithmétiques sont une collection de solutions numériques de 130 équations [...]

• CALCUL LITTÉRAL

  • Écrit par Olivier GENIN
  • 1 média
  

  On appelle calcul littéral un calcul qui s’effectue avec au moins un nombre dont la valeur est inconnue.Ce nombre est symbolisé par une lettre, souvent x ou y, d’où l’expression « calcul littéral », qui signifie « calcul avec des lettres ».La valeur de ce nombre étant inconnue, il est souvent appelé l’inconnue.Cette technique de calcul, qui « pose une inconnue », permet de résoudre de nombreux problèmes [...]

• CALCUL MENTAL

  • Écrit par Olivier GENIN
  • 1 média
  

  Le calcul mental, c'est résoudre des calculs « de tête », sans poser d'opération ni utiliser une calculatrice.Deux personnes n’auront pas forcément utilisé les mêmes raccourcis ou chemin de calcul pour trouver le bon résultat d’une opération. Pour résoudre « de tête » un calcul, il faut manier parfaitement « mentalement » les 4 opérations de base : l’addition, la soustraction, la multiplication et la division [...]

• CALCULS STATISTIQUES

  • Écrit par Olivier GENIN

  La statistique est la science mathématique qui consiste à récolter et à analyser des données chiffrées, afin de les commenter et de pouvoir observer des tendances.Les instituts de sondage sont des organismes qui utilisent la statistique pour décrire, par exemple, l’économie d’un pays, sa démographie, les tendances politiques ou encore la consommation des personnes concernant divers produits [...]

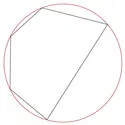
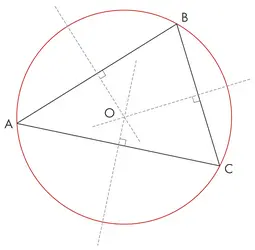
• CERCLE CIRCONSCRIT

  • Écrit par Olivier GENIN
  • 3 médias
  

  Un cercle circonscrit à un polygone est un cercle qui, s’il existe, passe par tous les sommets de ce polygone. À l’inverse, un cercle inscrit dans un polygone est un cercle qui, s’il existe, est tangent à chaque côté du polygone. On ne s’intéresse ici qu’au cas du cercle circonscrit à un triangle rectangle. Soit un cercle c de centre O et [BC] un diamètre du cercle [...]

• CERCLE

  • Écrit par Alain MATTHÈS

  Un cercle (du latin circus, « cercle », qui a aussi donné « cirque ») est une courbe plane fermée constituée des points situés à égale distance d’un point nommé centre. Il partage le plan en 2 régions, l’intérieur et l’extérieur. On utilise un compas pour le dessiner. C’est une forme simple de la géométrie euclidienne. La région du plan limitée par un cercle est appelée disque [...]

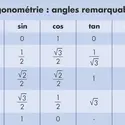
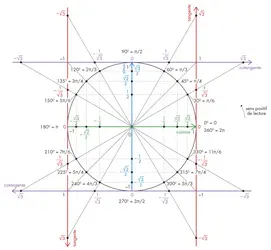
• CERCLE TRIGONOMÉTRIQUE

  • Écrit par Olivier GENIN
  • 2 médias
  

  Un cercle trigonométrique est un cercle de rayon 1 orienté positivement. Le sens positif est le sens contraire de celui des aiguilles d’une montre. Représentons un quart de cercle trigonométrique pour des angles aigus, notés x, tels que 00 ≤ x ≤ 900: Le rayon vertical, gradué de 0 au centre à 1 sur le cercle, est l’axe de lecture des sinus [...]

• CHASLES RELATION DE

  • Écrit par Olivier GENIN
  • 1 média
  

  La relation de Chasles porte le nom d'un mathématicien français du 19e siècle : Michel Chasles. En géométrie, elle permet de dire que, pour tout point A, B, C quelconque, l'égalité AB + BC = AC est vérifiée. Cela revient à dire que le vecteur AC est la somme des vecteurs AB et BC. Cependant, pour les longueurs, l'égalité [...]

• COMPARAISON, mathématiques

  • Écrit par Olivier GENIN
  • 2 médias
  

  La comparaison de 2 nombres réels permet de déterminer lequel est le plus grand et lequel est le plus petit. Pour comparer 2 nombres a et b, on les soustrait et on regarde si le résultat est positif, négatif ou nul : Si a - b > 0, alors a est strictement plus grand que b. Si a - b < 0, alors a est strictement plus petit que b [...]

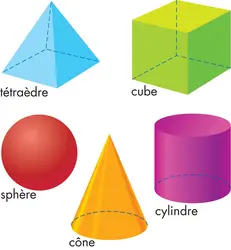
• CUBE

  • Écrit par Alain MATTHÈS

  Le cube (du grec kubos, « dé à jouer ») est un volume, ou solide, fondamental de l’espace que les géomètres analysent depuis des milliers d’années. Il est l’un des 5 solides de Platon, philosophe grec qui étudia des solides remarquables par leur esthétisme et leur symétrie. Le cube fait partie de plusieurs familles de solides. Le cube appartient à la grande famille des polyèdres [...]

• CYLINDRE

  • Écrit par Alain MATTHÈS

  En mathématiques, un cylindre est un volume fondamental de l’espace. Les grecs appelaient kylindros, devenu en français « cylindre » par l’intermédiaire du latin cylindrus, un rouleau q’ils utilisaient pour manœuvrer des charges très lourdes. De nombreux solides ont la forme de cylindre : une boîte de conserve, une craie pour écrire au tableau ou bien une colonne de temple [...]

• DÉMONSTRATION, mathématiques

  • Écrit par Bernard PIRE

  En mathématique, une démonstration est un discours qui permet d’établir la vérité d’une proposition à partir d’une ou de plusieurs hypothèses. Pour être valide, ce raisonnement doit respecter les lois de la logique. En général, la démonstration d’un résultat mathématique s’appuie sur des connaissances précédemment établies dans un domaine particulier des mathématiques [...]

• DÉPLACEMENTS, mathématiques

  • Écrit par Olivier GENIN

  En géométrie, un déplacement est une transformation qui garde les propriétés de la forme initiale déplacée. Un déplacement conserve les formes (une droite donne une droite, un carré donne un carré, etc.). Il conserve les mesures (longueurs, angles, aires). Il conserve les propriétés géométriques des figures (conservation des parallèles et des perpendiculaires, etc [...]

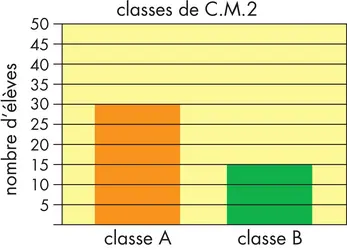
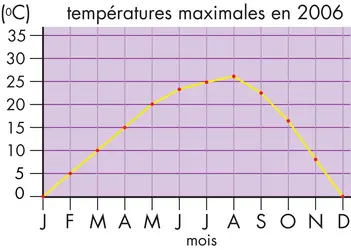
• DIAGRAMME

  • Écrit par Encyclopædia Universalis
  • 3 médias
  

  Les diagrammes, ou graphiques, sont des dessins représentant des informations mathématiques par des lignes, des formes et des couleurs. Ils permettent de comparer des quantités ou des chiffres et peuvent être compris plus facilement que des nombres et des mots. Il existe plusieurs types de diagrammes : circulaires, en bâtons et linéaires notamment [...]

• DISTRIBUTIVITÉ

  • Écrit par Alain MATTHÈS

  La distributivité (du latin distribuere, « répartir ») est une propriété de la multiplication par rapport à l’addition qui permet de passer d’un produit de sommes à une somme de produits. Une pièce rectangulaire de 13 mètres de longueur et de 5 mètres de largeur a pour superficie 65 mètres carrés, car 13 × 5 = 65. On peut la décomposer en 2 pièces rectangulaires dont l’une a 6 mètres et l’autre 7 mètres de longueur [...]

• DIVISION

  • Écrit par Alain MATTHÈS

  La division (du latin dividere, signifiant « partager ») est l’une des 4 opérations de l’arithmétique élémentaire. Elle permet de partager ou de répartir en plusieurs parties égales. Elle associe à 2 nombres entiers naturels, appelés dividende et diviseur, un entier appelé quotient. Le nombre à diviser est le dividende. Celui qui exprime en combien de parties égales on le divise se nomme diviseur ; ce dernier ne peut jamais être 0 [...]

• DROITE ÉQUATION DE

  • Écrit par Olivier GENIN

  Une droite est un ensemble illimité de points. Pour la représenter géométriquement, il faut définir un repère, connaître les coordonnées d’au moins 2 de ses points ou son équation. Le repère Dans le plan, un repère a 2 axes, qu'on appelle axe des abscisses pour l’axe horizontal et axe des ordonnées pour l’axe vertical. Le point d'intersection est l'origine du repère et se note généralement O [...]

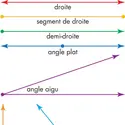
• DROITES REMARQUABLES DANS LE TRIANGLE

  • Écrit par Olivier GENIN

  Une droite est dite remarquable dans un triangle lorsqu’elle possède une ou plusieurs propriétés quel que soit le triangle. Il existe 4 types de droites remarquables dans le triangle : la médiane, la médiatrice, la hauteur et la bissectrice. Médianes dans le triangle La médiane est la droite qui passe par le milieu d’un côté du triangle et par le sommet opposé à ce côté [...]

• FONCTION, mathématiques

  • Écrit par Alain MATTHÈS

  Dans le langage courant, la notion de fonction impose une dépendance entre 2 quantités, par exemple dans l’expression « le prix est fonction de la demande ». En mathématiques, ce mot fut d’abord utilisé comme un mot du langage courant, pour indiquer qu’une quantité dépend d’une autre. Il fallut attendre le 19e siècle pour qu’on en donne une définition précise [...]

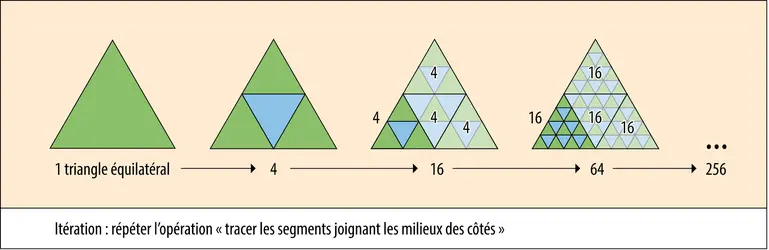
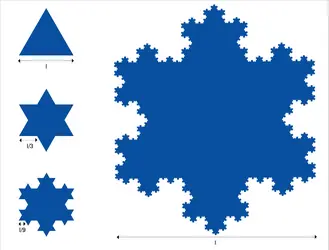
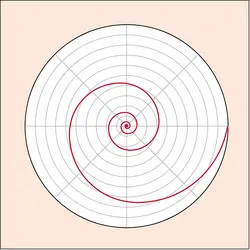
• FRACTALE

  • Écrit par Olivier GENIN
  • 3 médias
  

  Une « fractale », ou objet fractal, présente des motifs identiques à diverses échelles. Le tout est similaire à une de ses parties, et cela au niveau du moindre détail. En mathématiques, une fractale désigne une courbe ou une surface irrégulière ou éclatée mais qui obéit à des règles déterministes (l’évolution de la forme est causée par des états antérieurs), notamment une homothétie interne [...]

• FRACTION

  • Écrit par Olivier GENIN
  • 1 média
  

  Une fraction est une division de 2 nombres entiers relatifs. Son résultat est appelé le quotient : a ∈ (ensemble des nombres entiers relatifs) et b ∈ * (ensemble des entiers relatifs non nuls).Les fractions font parties de la famille des nombres rationnels, notés .La partie au-dessus du trait de fraction, le dividende, est appelée le numérateur [...]

• GÉOMÉTRIE

  • Écrit par Encyclopædia Universalis
  • 3 médias
  

  La géométrie est une science mathématique qui étudie les formes et les figures. Elle explique comment construire ou dessiner, mesurer et comparer des formes. On utilise notamment la géométrie pour bâtir des maisons et des ponts, mais aussi pour organiser des voyages dans l’espace. Points, droites et angles La géométrie repose sur les notions de point, de droite et d’angle [...]

• HOMOTHÉTIE

  • Écrit par Olivier GENIN

  Une homothétie est la transformation de centre O et de rapport k qui à tout point M associe le point M’ tel que : OM’ = kOM .La notation est : hO,k(M) = M’ ou hO,k : M → M’. M’ est l’image de M, et k est le rapport, c’est-à-dire la proportion entre le vecteur final et le vecteur initial [...]

• IDENTITÉS REMARQUABLES

  • Écrit par Olivier GENIN

  Les identités remarquables permettent de pouvoir factoriser et développer des expressions mathématiques de manière plus simple. Les expressions qui se trouvent à gauche du signe égal (=) sont les produits remarquables : ce sont les formes factorisées. Les expressions qui se trouvent à droite du signe égal sont les sommes remarquables : ce sont les formes développées [...]

• INFINI, mathématiques

  • Écrit par Olivier GENIN
  • 1 média
  

  Littéralement, le mot « infini » sert à qualifier quelque chose qui est sans limite. Les premières définitions de l’infini furent d’ailleurs des définitions dites négatives. Pour les Grecs et les Romains, « l’infini, c’est tout ce qui n’est pas fini ». Pour Aristote, c’est « ce qui ne se laisse pas parcourir et n’a pas de limite ». Encore aujourd’hui, l’infini est couramment défini comme ce que ce n’est pas [...]

• ITÉRATION, mathématiques

  • Écrit par Bernard PIRE
  • 1 média
  

  Itérer une opération mathématique, c’est la répéter un certain nombre de fois en prenant le résultat précédent comme point de départ de l’opération suivante. Par exemple, si on itère l’opération « multiplier par 3 » en commençant par le nombre 2, on obtient successivement 6, 18, 54, 162,...Itérer une opération revient souvent à définir une nouvelle opération [...]

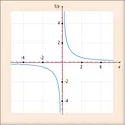
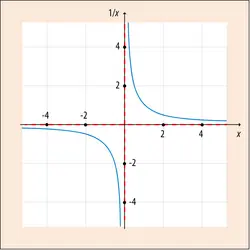
• LIMITE, mathématiques

  • Écrit par Bernard PIRE
  • 2 médias
  

  En mathématiques, on utilise le terme « limite » principalement lors des études de fonctions numériques. Trouver la limite en un point particulier d’une fonction, c’est déterminer de quelle valeur elle s’approche lorsque la variable s’approche (sans l’atteindre) de ce point particulier. Trouver la limite à l’infini d’une fonction, c’est déterminer de quelle valeur celle-ci s’approche lorsque la variable croît indéfiniment [...]

• LONGUEUR

  • Écrit par Alain MATTHÈS

  La longueur d’un objet, qui permet d’évaluer sa grandeur, est la distance entre ses 2 extrémités les plus éloignées. En géométrie, la longueur est souvent opposée à la largeur. Le mot « oblong » sert à caractériser des objets plus longs que larges. Communément, la longueur d’un objet fait partie de ses dimensions, tout comme la largeur, la hauteur ou encore l’épaisseur, voire comme un diamètre pour un objet de révolution [...]

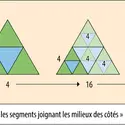
• MILIEUX THÉORÈME DE

  • Écrit par Olivier GENIN

  Le théorème des milieux dit que, dans un triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté. Soit ABC un triangle, soit I le milieu du segment [AB]. Si J est le milieu du segment [AC], alors la droite (IJ) est parallèle à la droite (BC) : La réciproque est vraie : dans un triangle, la droite parallèle à un côté qui passe par le milieu [...]

• MODÉLISATION, mathématiques

  • Écrit par Bernard PIRE
  • 2 médias
  

  En mathématiques, la modélisation est la représentation de toutes sortes de situations, d'objets et de structures du monde réel. L'étude mathématique de ces représentations, qui contient une bonne part de simulations informatiques, nous informe sur le monde réel. Il faut distinguer les situations où la modélisation se fonde sur des lois physiques bien établies, et celles dont les bases mêmes sont [...]

• MULTIPLICATION

  • Écrit par Alain MATTHÈS

  La multiplication (du latin multiplicatio, qui signifie « augmentation ») est l’une des 4 opérations de l’arithmétique élémentaire. Multiplier un nombre entier par un autre, c’est ajouter cet entier à lui-même plusieurs fois. Lorsque les nombres à ajouter entre eux sont égaux, l’addition prend le nom de multiplication. Ajouter 3 fois un nombre, c’est tripler ce nombre [...]

• NAPOLÉON THÉORÈME DE

  • Écrit par Olivier GENIN
  • 1 média
  

  Le théorème de Napoléon dit que, si l’on forme 3 triangles équilatéraux à partir des cotés d’un triangle quelconque, alors les centres de gravité de ces 3 triangles (points d’intersection des médianes) forment à leur tour un triangle équilatéral.Construisons un triangle ABC, quelconque, puis extérieurement, 3 triangles équilatéraux ABM, BCP et ACN. Si les points G, H et I désignent les centres de [...]

• NOMBRE D'OR

  • Écrit par Olivier GENIN
  • 3 médias
  

  Le nombre d’or est égal approximativement à 1,618 033 988 7. Mais, bien plus qu’une valeur, ce chiffre correspond avant tout à une proportion, la « proportion d’or ». Cette proportion est réalisée quand 2 longueurs strictement positives a et b respectent l’égalité suivante :Le nombre d’or est égal à a/b et correspond à l’unique racine positive de l’équation ci-dessus [...]

• NOMBRE DÉCIMAL

  • Écrit par Alain MATTHÈS

  En mathématiques, un nombre décimal s’écrit à l’aide d’une virgule, suivie d’un nombre fini de chiffres. L’existence du zéro en tant que chiffre a permis la création du système décimal, dans lequel un nombre s’écrit à l’aide des 10 chiffres (de 0 à 9) et des groupements qui se font par 10 : la dizaine (10 unités), la centaine (10 dizaines), le millier (10 centaines), etc [...]

• NOMBRE ENTIER RELATIF

  • Écrit par Alain MATTHÈS

  En mathématiques, un nombre entier relatif se compose d’un entier naturel précédé d’un signe positif (+) ou négatif (-). Les entiers positifs s’identifient aux entiers naturels (1, 2, 3, etc.), tandis que les entiers négatifs sont leurs opposés (- 1, - 2, - 3, etc.). Le chiffre 0 fait aussi partie des nombres entiers relatifs, mais il est dépourvu de signe [...]

• NOMBRE ENTIER

  • Écrit par Alain MATTHÈS

  En mathématiques, un nombre entier est un nombre naturel positif (1, 2, 3, etc.) ou un nombre nul (0) permettant de compter des objets distincts. L’étude des entiers, avec notamment les opérations d’addition et de multiplication, constitue une branche élémentaire des mathématiques appelée arithmétique. Les nombres sont écrits à l’aide de chiffres. De nombreuses civilisations (notamment [...]

• NOMBRES ET NOTATION NUMÉRALE

  • Écrit par Encyclopædia Universalis
  • 3 médias
  

  Un nombre est un concept de base en mathématique, servant à compter, à mesurer et à comparer des quantités. Un système de notation numérale est un ensemble de symboles représentant des nombres. Le système de notation numérale le plus courant recourt à 10 symboles, les chiffres (0, 1, 2, 3, 4, 5, 6, 7, 8, et 9), utilisés seuls ou en combinaisons. Types de nombres Les nombres peuvent être classés de plusieurs manières [...]

• NOMBRES INVERSES ET OPPOSÉS

  • Écrit par Olivier GENIN

  Souvent, les notions d’inverse et d’opposé en mathématiques prêtent à confusion.Deux nombres réels opposés sont 2 nombres qui ont la même partie numérique, mais des signes différents. Leurs distances par rapport à l’origine O d’un axe sont égales, mais opposées. Ainsi, sur un axe horizontal gradué, zéro est au centre du segment [– aa] formé par 2 nombres opposés [...]

• NOMBRES PARFAITS

  • Écrit par Olivier GENIN
  • 1 média
  

  Un nombre parfait est un nombre entier naturel dont la somme des diviseurs propres (diviseurs différents du nombre lui-même) est égale à ce nombre. Par exemple, 6 est divisible par 1, 2 et 3, et 6 = 1 + 2 + 3.Dès l’Antiquité, au 3e siècle av. J.-C., Euclide expérimentait les nombres parfaits. Au 17e siècle, Euler reprend les travaux d’Euclide et prouve une formule pour les nombres parfaits pairs [...]

• NOMBRES PREMIERS

  • Écrit par Olivier GENIN
  • 1 média
  

  Un nombre premier est un nombre entier supérieur ou égal à 2 et divisible uniquement par 1 et par lui-même pour donner un nombre entier : 2 est le seul nombre premier pair. Il existe une infinité de nombres premiers, qui sont donc tous impairs.L’étude des nombres premiers fait partie de la branche des mathématiques appelée l’arithmétique.C’est le mathématicien grec Euclide qui, au 3e siècle av [...]

• OPÉRATIONS, mathématiques

  • Écrit par Olivier GENIN

  Les 4 opérations mathématiques élémentaires sont l’addition, la soustraction, la multiplication et la division. Les symboles respectifs sont +, –, × et : ; ils sont appelés opérateurs. Les chiffres ou les variables qu’ils font intervenir sont appelés opérandes. La mise à la puissance d’un opérande est aussi une opération mathématique.Addition et soustraction Pour effectuer une suite d’additions [...]

• PARALLÈLE

  • Écrit par Alain MATTHÈS

  En géométrie euclidienne, le parallélisme est une propriété relative aux droites. Ainsi, 2 droites dans un plan sont dites parallèles si elles n’ont aucun point commun ou si elles sont confondues. Dans le cas contraire, les droites n’ont qu’un et un seul point commun. Elles sont alors dites sécantes. La géométrie euclidienne a débuté avec les Éléments, ensemble de 13 livres probablement écrits par le mathématicien grec Euclide [...]

• PAVAGE

  • Écrit par Olivier GENIN
  • 1 média
  

  Paver un plan, c'est recouvrir entièrement ce plan, sans laisser de trou ni faire de superposition, avec une forme de base appelée pavé de base, qu'on reproduit autant qu'on veut en lui faisant subir des transformations simples et répétées. Le pavage peut être géométrique, les formes faisant appel à des polygones simples ou plus ou moins complexes [...]

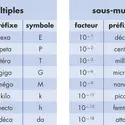
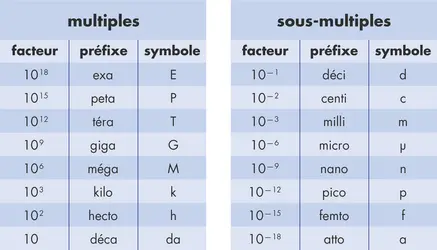
• PÉRIMÈTRE ET AIRE

  • Écrit par Olivier GENIN
  • 3 médias
  

  Le périmètre est la mesure de la longueur des contours d’une forme géométrique dans le plan, c'est-à-dire en 2 dimensions, le plus souvent appelées longueur et largeur. L’unité de mesure est le mètre (noté m), avec ses multiples et sous-multiples. L’aire est la mesure de la surface de la forme géométrique. L’unité de mesure est le mètre carré (noté m2), avec ses multiples et sous-multiples [...]

• PÉRIMÈTRE

  • Écrit par Alain MATTHÈS

  En géométrie, le périmètre désigne à la fois la longueur du contour d’une surface, mais aussi la ligne qui ferme cette surface. Ce mot est construit à partir du préfixe péri- (« autour ») et du suffixe -mètre (« mesure »). Le périmètre est, avec l’aire, l’une des mesures principales des figures géométriques. Une surface comme un disque est limitée par une ligne, le cercle [...]

• PERPENDICULAIRE

  • Écrit par Alain MATTHÈS

  En géométrie plane, 2 droites non parallèles sont toujours sécantes (elles se coupent en un point). Elles sont dites perpendiculaires (du latin perpendiculum, « fil à plomb ») lorsqu’elles se coupent en formant un angle droit. Cette définition est aussi valable dans l’espace. On code cette caractéristique par un petit carré à l’intersection des 2 droites [...]

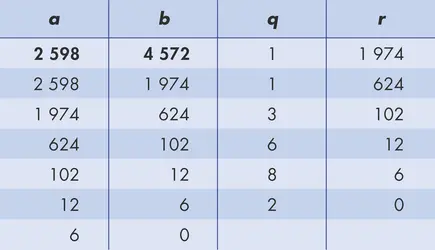
• PGCD ET PPCM

  • Écrit par Olivier GENIN
  • 1 média
  

  Le PGCD et le PPCM sont, respectivement, le plus grand commun diviseur et le plus petit commun multiple entre 2 nombres entiers naturels.Le PGCDLe PGCD de 2 nombres entiers naturels a et b (a, b ∈ ) correspond donc au plus grand nombre k qui divise à la fois a et b :etLe PGCD permet notamment de simplifier les fractions complexes [...]

• PI

  • Écrit par Olivier GENIN
  • 2 médias
  

  Le nombre pi (noté π) est le nombre défini par l’aire du disque ou le périmètre du cercle : – pi est le rapport entre la circonférence du cercle (le périmètre p) et son diamètre D (2 fois le rayon r) :– pi est aussi le rapport entre l’aire du disque (A) et son rayon (r) au carré : La valeur approchée admise de π est 3,141 59 [...]

• POURCENTAGE

  • Écrit par Alain MATTHÈS

  Un pourcentage est un rapport entre 2 nombres qui s’exprime sous la forme d’une fraction dont le dénominateur est 100. Pour mesurer l’importance d’une partie quantifiable ayant une caractéristique particulière par rapport à un ensemble auquel elle appartient, on utilise un rapport. Par exemple, si dans 20 centilitres d’une boisson il y a 5 centilitres de jus d’orange, alors un quart (5/20) de cette boisson est constituée de jus d’orange [...]

• PROJECTION ET RÉFLEXION, mathématiques

  • Écrit par Olivier GENIN
  • 2 médias
  

  En géométrie, la projection et la réflexion sont 2 transformations qui ne gardent pas les propriétés de la forme initiale déplacée. En cela, elles s’opposent aux déplacements que sont la translation, la rotation, la symétrie axiale et la symétrie centrale. La projection Une projection est une image d’une figure ou d’un objet, projetée sur un support, un plan donné [...]

• PROPORTIONNALITÉ

  • Écrit par Alain MATTHÈS

  En sciences, la proportionnalité est le caractère par lequel 2 grandeurs mesurables restent dans le même rapport. Par exemple, en mathématiques, lorsque le diamètre d’un cercle double, la circonférence double. La proportionnalité entre 2 grandeurs peut être établie par l’égalité de rapports de 2 quantités de même type. Le terme « proportion », concept qui appartient à l’héritage grec, s’applique aux éléments quantifiables [...]

• PUISSANCE, mathématiques

  • Écrit par Olivier GENIN
  • 1 média
  

  La puissance n-ième d’un nombre a est : (a est multiplié par lui-même n fois, on a donc n facteurs). an se dit « a puissance n » ou « a exposant n ».L’exposant n est un nombre entier non nul.Un nombre à l’exposant 1 ne change pas le nombre :Un nombre à l’exposant 0 est toujours [...]

• PYTHAGORE THÉORÈME DE

  • Écrit par Olivier GENIN
  • 1 média
  

  Le théorème de Pythagore dit que, dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. Dans un triangle rectangle, le côté opposé à l’angle droit est appelé l’hypoténuse. L’hypoténuse est toujours le plus grand des côtés Soit ABC un triangle rectangle en A, alors on a : BC2 = AB2 + AC2 [...]

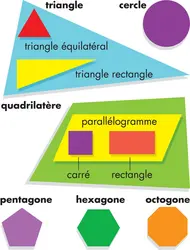
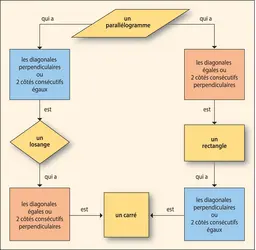
• QUADRILATÈRE

  • Écrit par Alain MATTHÈS

  Le quadrilatère est une figure géométrique possédant 4 côtés. Il fait partie de la famille des polygones, figures ayant plusieurs angles. Un quadrilatère noté ABCD possède 4 sommets, qui sont les points A, B, C et D, et 4 côtés, qui sont les segments [AB], [BC], [CD] et [DA]. Il possède aussi 2 diagonales, qui joignent les sommets opposés et sont les segments [AC] et [BD] [...]

• RACINE CARRÉE

  • Écrit par Olivier GENIN
  • 1 média
  

  La racine carrée d’un nombre strictement positif a est le nombre positif, noté , qui, élevé au carré, donne a : La racine carrée d’un nombre au carré, est égale à ce nombre : La racine carrée d’un nombre négatif n’existe pas : .En revanche, et existent.Le produit de 2 racines carrées est égal à la racine carrée du produit :Le quotient de 2 racines carrées est égal à la racine [...]

• RÈGLE DE TROIS

  • Écrit par Alain MATTHÈS

  La règle de trois est une méthode de calcul qui fait intervenir 3 valeurs pour en obtenir une quatrième. Les 3 nombres a, b et c étant donnés, il s’agit de déterminer un nombre d tel que a et b soient proportionnels à c et d. On appelle quatrième proportionnelle le quatrième nombre d [...]

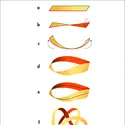
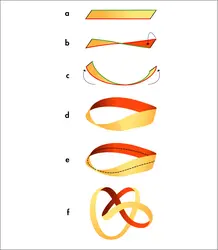
• RUBAN DE MÖBIUS, mathématiques

  • 2 médias
  

  Un ruban de Möbius est une surface n’ayant que 1 seule face et 1 seul bord. Pour permettre de visualiser cette caractéristique, on obtient facilement un ruban de Möbius en faisant subir 1 torsion d’un demi-tour à un ruban, puis en collant les 2 extrémités. C’est dans un mémoire, présenté à l'Académie des sciences mais qui ne fut découvert qu'après sa mort en 1868, que le mathématicien allemand [...]

• SCIENCE ET MÉTHODE SCIENTIFIQUE

  • Écrit par Encyclopædia Universalis
  • 2 médias
  

  La science est un vaste champ de recherche. Son but est de comprendre l’Univers, comment il s’est formé et tout ce qu’il contient.Branches de la scienceIl existe de nombreux sujets de recherche. Mais, la science peut être subdivisée en 3 grandes branches.Sciences physiquesLes sciences physiques sont axées sur la matière, de l’Univers entier aux particules infiniment petites qui constituent l’atome [...]

• SOUSTRACTION

  • Écrit par Alain MATTHÈS

  La soustraction (du latin substractio, qui signifie l’« action de se retirer ») est une des 4 opérations élémentaires de l’arithmétique. Elle consiste à retrancher un nombre d’un autre. On considère parfois que la soustraction est l’opposé de l’addition. Celle-ci consiste en effet à enlever un nombre au lieu de l’ajouter. Quand on veut ôter un nombre d’un autre, la première idée est de [...]

• STATISTIQUE

  • Écrit par Encyclopædia Universalis
  • 1 média
  

  La statistique est la branche des mathématiques qui consiste à recueillir, à traiter et à interpréter des informations. Les chiffres ainsi obtenus sont appelés les statistiques. Ils permettent d’établir des prévisions dans divers domaines (météo, compétitions sportives). Ils servent aussi à décrire des éléments spécifiques concernant des groupes de personnes (niveau d’alphabétisation, intentions de vote, poids moyens des habitants d’une ville) [...]

• SYMÉTRIE CENTRALE

  • Écrit par Olivier GENIN

  Une symétrie centrale est une transformation géométrique qui à chaque point associe un point image symétrique par rapport à un centre de symétrie. Si M’ est le symétrique de M par rapport à I alors M est le symétrique de M’ par rapport à I. On dit que M’ et M sont symétriques par rapport à I. Le symétrique de I est I. C’est le seul point dans ce cas [...]

• SYMÉTRIE

  • Écrit par Alain MATTHÈS

  En mathématiques, la symétrie (du latin symmetria, « justesse des proportions ») est une transformation géométrique qui ne provoque aucune modification de forme ni de dimensions. Dès l’Antiquité, les figures possédant des symétries ont fait l’objet d’intenses études. Le cercle, le triangle équilatéral, le carré et tous les autres polygones réguliers ont révélé d’intéressantes propriétés [...]

• THALÈS THÉORÈME DE

  • Écrit par Olivier GENIN

  Le théorème de Thalès dit que si (d) et (d’) sont deux droites sécantes en un point A, B et M deux points de la droite (d), distincts de A, C et N deux points de la droite (d’), distincts de A, et si les droites (BC) et (MN) sont parallèles, alors : La figure ABC forme un triangle. D’où l’énoncé restreint du théorème de Thalès, appliqué au triangle [...]

• TRIANGLE

  • Écrit par Alain MATTHÈS

  Le triangle est une figure géométrique élémentaire formée par 3 points et par les 3 segments qui les relient. Elle fait partie de la famille des polygones et a été nommée à une certaine époque « trigone », c’est à dire figure possédant 3 angles. Les mots « pentagone » et « trigonométrie » ont conservé leur racine grecque gonia, qui signifie « angle » [...]

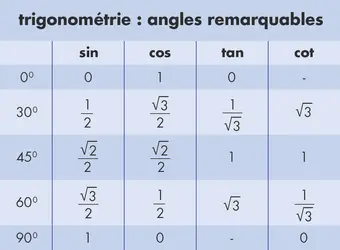
• TRIGONOMÉTRIE DANS LE TRIANGLE RECTANGLE

  • Écrit par Olivier GENIN
  • 1 média
  

  La trigonométrie étudie les relations existant entre les longueurs des côtés d’un triangle et les mesures de ses angles. La trigonométrie est utilisée depuis longtemps en astronomie, en géographie, et par les marins. L’hypoténuse est le coté opposé à l’angle droit. C’est toujours le plus grand des côtés dans un triangle rectangle.Le côté opposé et le côté adjacent sont les deux côtés de l’angle [...]

• VECTEUR, mathématiques

  • Écrit par Olivier GENIN

  Un vecteur est défini par son origine (ou point de départ), son extrémité (ou point d'arrivée), sa longueur, encore appelée norme du vecteur, sa direction, qui est celle de la droite qui le porte, et son sens, de son origine à son extrémité. Ainsi, le vecteur AB est défini par son origine (le point A), son extrémité (le point B), sa longueur AB, appelée norme et notée [...]

• VOLUME

  • Écrit par Alain MATTHÈS

  En mathématiques, le volume désigne à la fois la partie de l’espace qu’occupe un objet et sa mesure. Ce terme provient du latin voluminis (« chose enroulée »), formé à partir du verbe volvere, qu’on retrouve dans le mot « révolution ». Les objets de révolution sont obtenus par rotation autour d’un axe, par exemple un cylindre obtenu sur un tour à bois [...]

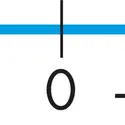
• ZÉRO

  • Écrit par Olivier GENIN
  • 1 média
  

  La notion de zéro, comme la notion d’infini, est difficile à cerner et à définir pour l’homme. Philosophiquement, le zéro est lié au néant, au vide. En théologie, zéro serait le moment juste avant la naissance de notre Univers. En physique, ce serait l’instant exact du big bang. En mathématiques, le zéro a été créé par nécessité, notamment pour des besoins de calculs arithmétiques [...]

Documents

Médias