Fabrication d’un ruban de Möbius
© Encyclopædia Universalis France
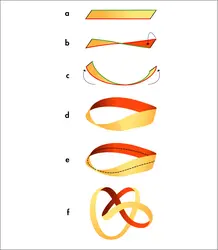
Un ruban de Möbius est une surface n’ayant que 1 seule face et 1 seul bord. Pour permettre de visualiser cette caractéristique, on obtient facilement un ruban de Möbius en faisant subir 1 torsion d’un demi-tour à un ruban, puis en collant les 2 extrémités.
Logo des matériaux recyclables
© R. Sotola/ Shutterstock
C’est dans un mémoire, présenté à l’Académie des sciences mais qui ne fut découvert qu’après sa mort en 1868, que le mathématicien allemand August Ferdinand Möbius discute les propriétés de surfaces unilatères, c’est-à-dire n’ayant que 1 seule face et 1 seule frontière. Il cite en particulier le paradoxal ruban qui porte son nom et qu’il a étudié en 1858 alors qu’il répondait à une question posée par l’Académie sur la géométrie des polyèdres. Le ruban de Möbius a de plus l’étrange propriété de rester d’une seule pièce lorsqu’on le coupe le long de sa ligne médiane. En fait le célèbre ruban avait été discuté peu de temps auparavant par le mathématicien allemand Johann Benedict[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
