Cadran solaire
© Frank Jr/ Shutterstock
En géométrie, la projection et la réflexion sont 2 transformations qui ne gardent pas les propriétés de la forme initiale déplacée. En[...]
La projection
Une projection est une image d’une figure ou d’un objet, projetée sur un support, un plan donné.
La projection n’est pas un déplacement, au sens mathématique, car elle modifie la forme et les mesures, en général, sauf quand elle est orthogonale (comme la projection d’un film sur un écran de cinéma).
La projection du segment[AB]sur la droite (d) suivant les vecteurs BB’ et AA’ donne comme image projetée le segment[A’B’], de longueur différente :
AB ≠ A’B’.
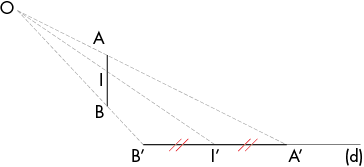
Ici, le point I’ est le milieu du segment[A’B’], mais I n’est pas le milieu[...]
La réflexion
En géométrie, la réflexion peut être définie comme le changement de direction d’une onde, lorsque celle-ci rencontre la surface d’un obstacle.
Le principe de la réflexion a été étudié par Descartes, notamment la réflexion d’un rayon lumineux sur un miroir.
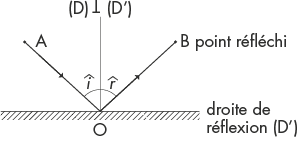
Selon le principe de la réflexion, un point B est le point réfléchi d’un point A par la réflexion d’angle AOB si AOB = i + r, où i = r avec i < 900 et r < 900.
i est l’angle incident formé du vecteur [...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
