Valeurs trigonométriques
© Encyclopædia Universalis France
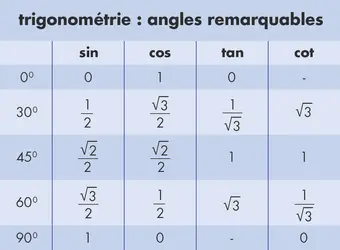
Un cercle trigonométrique est un cercle de rayon 1 orienté positivement. Le sens positif est le sens contraire de celui des aiguilles d’une montre.
Représentons un quart de cercle trigonométrique pour des angles aigus, notés x, tels que 00 ≤ x ≤ 900:
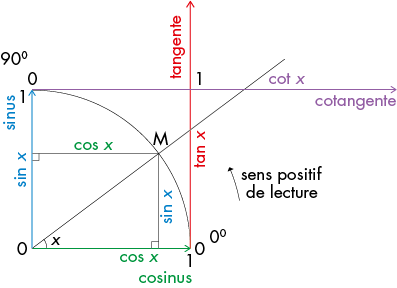
Le rayon vertical, gradué de 0 au centre à 1 sur le cercle, est l’axe de lecture des sinus.
0 ≤ sin x ≤ 1.
Le rayon horizontal, gradué de 0 au centre à 1 sur le cercle, est l’axe de lecture des cosinus.
0 ≤ cos x ≤ 1.
La tangente verticale au quart de cercle à l’extrémité du rayon des cosinus est l’axe de lecture des tangentes.
La tangente horizontale au quart de cercle à l’extrémité du rayon des sinus est l’axe de lecture des cotangentes.
La lecture des sinus et cosinus se fait dans le quart de cercle, contrairement à la lecture des tangentes et cotangentes, qui se fait en dehors du cercle.
Soit un point M sur le quart de cercle. On note x l’angle formé entre la droite passant par le centre du quart cercle et le point M, et le rayon horizontal des cosinus.
La valeur du cosinus de l’angle x est le point d’intersection entre la verticale issue de M et le rayon des cosinus.
La valeur du sinus de l’angle x est le point d’intersection entre l’horizontale issue de M et le rayon des sinus.
Le triangle formé par l’angle x et la verticale issue de M est un triangle rectangle, dont l’hypoténuse est un rayon du quart de cercle d’unité 1, et les cotés de l’angle droit sont le sinus et le cosinus.
D’après le théorème de Pythagore :
cos2x + sin2x = 1.
Pour lire la tangente et la cotangente, il suffit de prolonger le rayon passant par M à l’extérieur du cercle tel qu’il coupe les 2 tangentes.
La valeur de la tangente et de la cotangente se lira aux points d’intersection.
De la construction, il se déduit que pour tout angle x de mesure inférieure à 450, la tangente sera inférieure à 1 et la cotangente supérieure à 1 :
Si 00 < x < 450 alors 0 ≤ tan x < 1 et 1 < cot x.
Si x est égal à 450, alors la tangente est égale à la cotangente et vaut 1.
Si x = 450 alors tan x = cot x = 1.
Pour tout angle x de mesure supérieure à 450 et inférieure à 900, la tangente sera supérieure à 1 et la cotangente inférieure à 1 :
Si 450 < x < 900 alors 1 < tan x et 0 ≤ cot x < 1 .
Pour tout angle x de mesure égale à 00, l’angle nul, alors la tangente est égale à 0.
La droite de lecture des cotangentes, la tangente horizontale au cercle est parallèle au rayon de lecture des cosinus.
Les 2 sont horizontales. Cela signifie que, pour un angle nul, 00, la cotangente n’existe pas.
Si x = 00 alors tan x = 0 et cot x = ∅.
Pour tout angle x de mesure égale à 900, l’angle droit, alors la cotangente est égale à 0.
La droite de lecture des tangentes, la tangente au quart de cercle est parallèle au rayon de lecture des sinus.
Les 2 sont verticales. Cela signifie, que[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
