Le théorème des milieux dit que, dans un triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté.
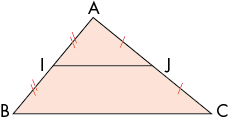
Soit ABC un triangle, soit I le milieu du segment[AB]. Si J est le milieu du segment[AC],
alors la droite (IJ) est parallèle à la droite (BC) :
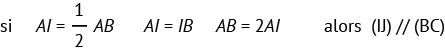
La réciproque est vraie : dans un triangle, la droite parallèle à un côté qui passe par le milieu d’un deuxième côté coupe le troisième côté en son milieu.
Soit ABC un triangle. Soit I le milieu du segment[AB]et J un point de la droite (AC). Si la droite (IJ) est parallèle à la droite (BC), alors J est milieu du segment[AC].
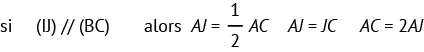
De plus, dans un triangle, le segment qui joint les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter


