Une symétrie centrale est une transformation géométrique qui à chaque point associe un point image symétrique par rapport à un centre de symétrie.
Si M’ est le symétrique de M par rapport à I alors M est le symétrique de M’ par rapport à I. On dit que M’ et M sont symétriques par rapport à I.
Le symétrique de I est I. C’est le seul point dans ce cas. I s’appelle le centre de symétrie.
Deux figures sont symétriques par rapport à un point O si elles se superposent après un demi-tour autour du point O, qui est centre de symétrie.
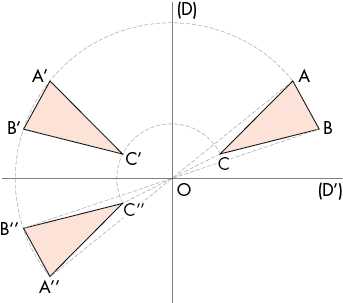
Le triangle A’’B’’C’’ est le symétrique du triangle ABC par la symétrie de centre O.
Le point O est le milieu des segments [AA’’], [BB’’] et [CC’’] : OA = OA’’, OB = OB’’, OC = OC’’ ; [AB] // [B’’A’’], [AC] // [C’’A’’], [CB] // [B’’C’’] ; Les triangles A’’B’’C’’ et ABC sont identiques.
Faire une symétrie centrale revient à faire un demi-tour, une rotation de 1800. Ici, les points A’’, B’’ et C’’ sont les images des points A, B et C par la rotation de centre O et de rayons respectifs OA, OB et OC.
Faire une[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter

