Le théorème de Thalès dit que si (d) et (d’) sont deux droites sécantes en un point A, B et M deux points de la droite (d), distincts de A, C et N deux points de la droite (d’), distincts de A, et si les droites (BC) et (MN) sont parallèles, alors :
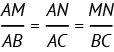
La figure ABC forme un triangle. D’où l’énoncé restreint du théorème de Thalès, appliqué au triangle.
Soit un triangle ABC; si une droite (MN) est parallèle au coté[BC], alors les égalités suivantes sont vérifiées :
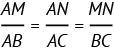
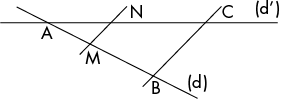
Il existe trois configurations de Thalès.
Dans la configuration dite en « papillon », les triangles ABC et AMN sont opposés par le sommet.
La droite (MN) passe en dehors du triangle ABC parallèlement à[BC], mais du côté opposé à[BC]par rapport au sommet A.
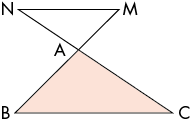
Dans une deuxième configuration, le triangle AMN est contenu dans le triangle ABC.
Le triangle AMN est alors une réduction du triangle ABC. La[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter


