En géométrie, un déplacement est une transformation qui garde les propriétés de la forme initiale déplacée. Un déplacement conserve les formes (une droite donne une droite, un carré donne un carré, etc.). Il conserve les mesures (longueurs, angles, aires).[...]
La translation
Une translation correspond à un glissement selon une direction dans le même sens, c’est-à-dire suivant un vecteur.
L’ image d’un point M par la translation de vecteur AB est le point M’, tel que les demi-droites[AB) et[MM’) soient parallèles et de mêmes sens.[AB]et[MM’]ont la même longueur. M’ est le translaté de M.
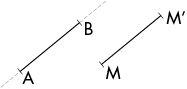
La translation est un glissement de longueur, sens et direction identiques de tous les points d’une figure, de telle sorte que la figure[...]
La rotation
Pour un point O et un angle α donnés, la rotation de centre O et d’angle α fait tourner un point M sur le cercle de centre O et de rayon OM, de telle sorte que l’angle MOM’ soit égal à l’angle α.
En mathématiques et en physique, le sens contraire des aiguilles d’une montre est appelé le « sens direct ».

On dit que M’ est l’image de M dans le sens[...]
Les symétries
La symétrie axiale (par rapport à une droite) fait correspondre à chaque point de la figure un autre point de la figure qu’on appelle image. L’ axe de symétrie est alors la médiatrice du segment défini par ces 2 points. Une figure est symétrique par rapport à une droite (l’axe de symétrie) si un pliage suivant[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter

