CHASLES RELATION DE
La relation de Chasles porte le nom d’un mathématicien français du 19e siècle : Michel Chasles.
En géométrie, elle permet de dire que, pour tout point A, B, C quelconque, l’égalité AB + BC = AC est vérifiée.
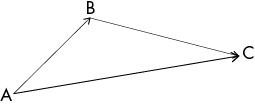
Cela revient à dire que le vecteur AC est la somme des vecteurs AB et BC.
Cependant, pour les longueurs, l’égalité AB + BC = AC est vraie seulement si le point B est sur le segment [AC].
On peut aussi utiliser la règle du parallélogramme :
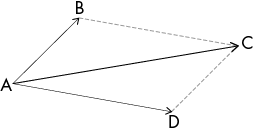
Si ABCD est un parallélogramme, alors AB + AD = AC.
En effet : comme AD = BC car c’est un parallélogramme, et que, d’après la relation de Chasles,
AB + BC = AC, alors AB + AD = AC.
Soit trois points I, J, et K. Construire le point L tel que IL = IJ + IK revient à construire le point I tel que IJLK soit un parallélogramme.
La suite de cet article est accessible aux abonnés
- Des contenus adaptés au niveau Junior
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Pour aller plus loin :
Articles liés
vecteur, mathématiques
Un vecteur est défini par son origine (ou point de départ), son extrémité (ou point d'arrivée), sa longueur, encore appelée norme du vecteur, sa direction, qui est celle de la droite qui le porte, et son sens, de son ... Lire l’article
