Hyperbole
© 2014 Encyclopædia Universalis
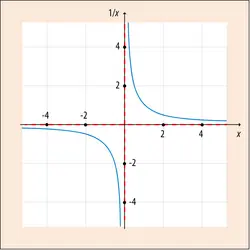
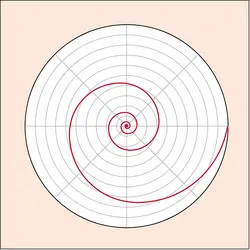
En mathématiques, on utilise le terme « limite » principalement lors des études de fonctions numériques. Trouver la limite en un point particulier d’une fonction, c’est déterminer de quelle valeur elle s’approche lorsque la variable s’approche (sans l’atteindre) de ce point particulier. Trouver la limite à l’infini d’une fonction, c’est déterminer de quelle valeur celle-ci s’approche lorsque la variable croît indéfiniment. La notion de limite apparaît aussi dans les constructions géométriques : la limite d’une courbe en spirale dont la distance à un point A diminue sans cesse jusqu’à devenir aussi petite que possible est le point A.
Spirale logarithmique
© 2014 Encyclopædia Universalis
C’est au 18e et au 19e siècle que la notion mathématique de limite a été précisée. Dans le cas des suites numériques, on dit qu’une suite est convergente si elle a une limite finie. Ainsi, la suite obtenue en divisant par 2 de façon répétée un nombre a (a/2, a/4, a/8, a/16...) converge vers le nombre 0. Lorsqu’on étudie une[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
