Une homothétie est la transformation de centre O et de rapport k qui à tout point M associe le point M’ tel que : OM’ = kOM .
La notation est : hO,k(M) = M’ ou hO,k : M → M’. M’ est l’image de M, et k est le rapport, c’est-à-dire la proportion entre le vecteur final et le vecteur initial.
Dans une homothétie, un point, son image et le centre de l’homothétie sont toujours alignés. Les vecteurs OM et OM’ sont colinéaires.
Si k < - 1, alors OM et OM’ sont de sens contraire et OM < OM’.
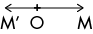
Si k = - 1, alors OM et OM’ sont de sens contraire et OM = OM’. Dans ce cas, c’est une symétrie centrale. Le point O est le milieu du segment [M’M]. Le point M’ est le symétrique du point M par rapport au point O centre de symétrie.
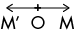
Si 0 < k < 1, alors OM et OM’ sont de même sens et OM’ < OM.
OM’ est donc une réduction de OM.
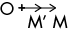
Si k = 1, alors OM et OM’ sont de même sens et OM = OM’.
Le point M et le point M’ sont confondus : c’est l’application identique. L’image du point est le point lui-même. M est donc invariant.
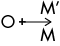
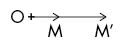
Si k > 1, alors OM et OM’ sont de même sens et OM’ > OM.
OM’ est donc un agrandissement de OM.
L’homothétie conserve les angles, le milieu, l’alignement, le parallélisme, les rapports de colinéarité, la forme des figures.[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter

