Pavage de Penrose
© 2005 Encyclopædia Universalis France S.A.
Paver un plan, c’est recouvrir entièrement ce plan, sans laisser de trou ni faire de superposition, avec une forme de base appelée pavé de base, qu’on reproduit autant qu’on veut en lui faisant subir des transformations simples et répétées.
Le pavage peut être géométrique, les formes faisant appel à des polygones simples ou plus ou moins complexes. Les pavages de Penrose (du nom du mathématicien britannique Roger Penrose) en sont une représentation.
Le pavage peut être figuratif, lorsque les pavés du plan sont des formes d’objets ou d’êtres réels, par exemple des feuilles de vignes ou des animaux. L’artiste néerlandais Maurits Cornelis Escher a ainsi fait un travail formidable sur les pavages
De l’Antiquité jusqu’à nos jours, les notions mathématiques et artistiques des pavages sont liées. On peut faire des pavages de manière artistique et intuitive sans connaître les notions mathématiques qu’on utilise pourtant.
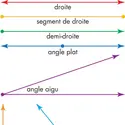
Les pavages utilisent, en effet, toutes les isométries vues en géométrie au[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
