géométrie
Article principal
-
- Écrit par Encyclopædia Universalis
- 3 médias
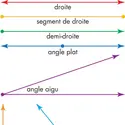
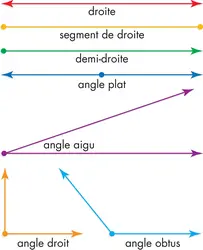
La géométrie est une science mathématique qui étudie les formes et les figures. Elle explique comment construire ou dessiner, mesurer et comparer des formes. On utilise notamment la géométrie pour bâtir des maisons et des ponts, mais aussi pour organiser des voyages dans l’espace. Points, droites et angles La géométrie repose sur les notions de point, de droite et d’angle [...]
Articles associés
-
AIRE - Écrit par Alain MATTHÈS
En géométrie, l’aire (du latin area, qui signifie « surface plane ») désigne la mesure d’une surface. En géographie, le terme « superficie » lui est préféré. Dans la langue de tous les jours, si une « surface » peut être cultivée, c’est la « superficie » cultivée qui est exprimée en hectares. Les Égyptiens savaient déjà évaluer les aires des figures planes comme le triangle, le rectangle ou le trapèze [...]
-
ANGLE ,géométrie - Écrit par Olivier GENIN
Un angle est une portion de plan délimité par deux droites sécantes en un point. Ce point d’intersection est appelé sommet de l’angle. La notation d’un angle, où le point O est le sommet de l’angle et les demi-droites [OA) et [OB) les côtés de l’angle, est AOB. Angles opposés Deux angles sont opposés par le sommet s’ils ont le même sommet et si leurs côtés sont dans le prolongement l’un de l’autre [...]
-
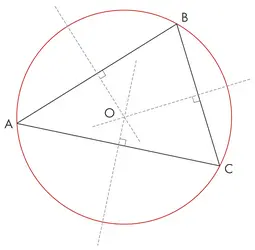
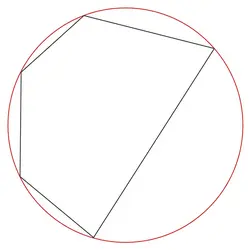
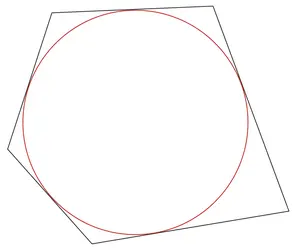
CERCLE CIRCONSCRIT - Écrit par Olivier GENIN
- 3 médias
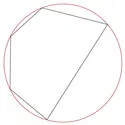
Un cercle circonscrit à un polygone est un cercle qui, s’il existe, passe par tous les sommets de ce polygone. À l’inverse, un cercle inscrit dans un polygone est un cercle qui, s’il existe, est tangent à chaque côté du polygone. On ne s’intéresse ici qu’au cas du cercle circonscrit à un triangle rectangle. Soit un cercle c de centre O et [BC] un diamètre du cercle [...]
-
CERCLE - Écrit par Alain MATTHÈS
Un cercle (du latin circus, « cercle », qui a aussi donné « cirque ») est une courbe plane fermée constituée des points situés à égale distance d’un point nommé centre. Il partage le plan en 2 régions, l’intérieur et l’extérieur. On utilise un compas pour le dessiner. C’est une forme simple de la géométrie euclidienne. La région du plan limitée par un cercle est appelée disque [...]
-
CHASLES, Michel (1793-1880)- Écrit par Olivier GENIN
Michel Chasles fut un mathématicien français du 19e siècle, essentiellement connu pour la célèbre relation qui porte son nom, utilisée dans le calcul vectoriel. C’est aussi lui qui inventa le mot « homothétie ». Michel Chasles naît le 15 novembre 1793 à Épernon, une petite ville située entre Rambouillet et Chartres. Son père, marchand de bois, fut président de la chambre de commerce [...]
-
CHASLES RELATION DE- Écrit par Olivier GENIN
- 1 média
La relation de Chasles porte le nom d'un mathématicien français du 19e siècle : Michel Chasles. En géométrie, elle permet de dire que, pour tout point A, B, C quelconque, l'égalité AB + BC = AC est vérifiée. Cela revient à dire que le vecteur AC est la somme des vecteurs AB et BC. Cependant, pour les longueurs, l'égalité [...]
-
CONWAY, John Horton (1937-2020)- Écrit par Olivier GENIN
John Horton Conway est un célèbre mathématicien britannique. Il est notamment connu pour ses travaux en théorie des jeux et en théorie des nombres.John Horton Conway naît le 26 décembre 1937 à Liverpool, en Grande-Bretagne. C’est pendant ses études qu’il se découvre une passion pour les jeux. Il obtient son doctorat en 1964 et devient professeur à l’université de Cambridge [...]
-
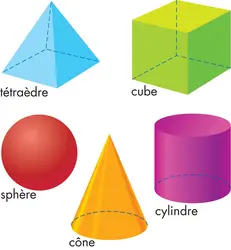
CUBE - Écrit par Alain MATTHÈS
Le cube (du grec kubos, « dé à jouer ») est un volume, ou solide, fondamental de l’espace que les géomètres analysent depuis des milliers d’années. Il est l’un des 5 solides de Platon, philosophe grec qui étudia des solides remarquables par leur esthétisme et leur symétrie. Le cube fait partie de plusieurs familles de solides. Le cube appartient à la grande famille des polyèdres [...]
-
CYLINDRE - Écrit par Alain MATTHÈS
En mathématiques, un cylindre est un volume fondamental de l’espace. Les grecs appelaient kylindros, devenu en français « cylindre » par l’intermédiaire du latin cylindrus, un rouleau q’ils utilisaient pour manœuvrer des charges très lourdes. De nombreux solides ont la forme de cylindre : une boîte de conserve, une craie pour écrire au tableau ou bien une colonne de temple [...]
-
DÉPLACEMENTS ,mathématiques - Écrit par Olivier GENIN
En géométrie, un déplacement est une transformation qui garde les propriétés de la forme initiale déplacée. Un déplacement conserve les formes (une droite donne une droite, un carré donne un carré, etc.). Il conserve les mesures (longueurs, angles, aires). Il conserve les propriétés géométriques des figures (conservation des parallèles et des perpendiculaires, etc [...]
-
DROITE ÉQUATION DE- Écrit par Olivier GENIN
Une droite est un ensemble illimité de points. Pour la représenter géométriquement, il faut définir un repère, connaître les coordonnées d’au moins 2 de ses points ou son équation. Le repère Dans le plan, un repère a 2 axes, qu'on appelle axe des abscisses pour l’axe horizontal et axe des ordonnées pour l’axe vertical. Le point d'intersection est l'origine du repère et se note généralement O [...]
-
DROITES REMARQUABLES DANS LE TRIANGLE - Écrit par Olivier GENIN
Une droite est dite remarquable dans un triangle lorsqu’elle possède une ou plusieurs propriétés quel que soit le triangle. Il existe 4 types de droites remarquables dans le triangle : la médiane, la médiatrice, la hauteur et la bissectrice. Médianes dans le triangle La médiane est la droite qui passe par le milieu d’un côté du triangle et par le sommet opposé à ce côté [...]
-
EUCLIDE (325?-265 av. J.-C.)- Écrit par Emmanuelle GRUNDMANN
Euclide fut un mathématicien de la Grèce antique. Il est l’auteur d’une œuvre en 13 tomes, Les Éléments, considérée comme le texte fondateur des mathématiques. Comme pour beaucoup de personnages de cette époque, on sait peu de choses de la vie d’Euclide. Il naquit probablement vers 325 av. J.-C. à Athènes et il mourut en 265 av. J.-C. en Égypte, où il était parti enseigner les mathématiques [...]
-
FIBONACCI, Leonardo (1170 env.- 1250 env.)- Écrit par Olivier GENIN
- 3 médias
Léonard de Pise (Leonardo Bigollo), plus connu sous le nom de Fibonacci, fut un mathématicien italien du 12e et du 13e siècle. Il est renommé pour ses travaux et écrits sur la théorie des nombres et la géométrie. Fibonacci naît vers 1170 à Pise. Il part pour l’Afrique du Nord rejoindre son père, responsable du bureau des douanes à Bejaïa, vers 1192 [...]
-
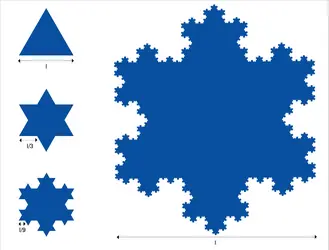
FRACTALE - Écrit par Olivier GENIN
- 3 médias
Une « fractale », ou objet fractal, présente des motifs identiques à diverses échelles. Le tout est similaire à une de ses parties, et cela au niveau du moindre détail. En mathématiques, une fractale désigne une courbe ou une surface irrégulière ou éclatée mais qui obéit à des règles déterministes (l’évolution de la forme est causée par des états antérieurs), notamment une homothétie interne [...]
-
HÉRON D'ALEXANDRIE (Ier s.?)- Écrit par Olivier GENIN
- 1 média
Héron d'Alexandrie, encore appelé Héron l'Ancien, fut un géomètre et inventeur grec du 1er siècle apr. J.-C. Il vécut à Alexandrie (Égypte). Il a transmis les connaissances mathématiques et techniques de Babylone et du monde gréco-romain. On lui attribue, entre autres, l'invention de la pompe aspirante et foulante, et la première machine à vapeur [...]
-
HOMOTHÉTIE - Écrit par Olivier GENIN
Une homothétie est la transformation de centre O et de rapport k qui à tout point M associe le point M’ tel que : OM’ = kOM .La notation est : hO,k(M) = M’ ou hO,k : M → M’. M’ est l’image de M, et k est le rapport, c’est-à-dire la proportion entre le vecteur final et le vecteur initial [...]
-
INFINI ,mathématiques - Écrit par Olivier GENIN
- 1 média
Littéralement, le mot « infini » sert à qualifier quelque chose qui est sans limite. Les premières définitions de l’infini furent d’ailleurs des définitions dites négatives. Pour les Grecs et les Romains, « l’infini, c’est tout ce qui n’est pas fini ». Pour Aristote, c’est « ce qui ne se laisse pas parcourir et n’a pas de limite ». Encore aujourd’hui, l’infini est couramment défini comme ce que ce n’est pas [...]
-
LONGUEUR - Écrit par Alain MATTHÈS
La longueur d’un objet, qui permet d’évaluer sa grandeur, est la distance entre ses 2 extrémités les plus éloignées. En géométrie, la longueur est souvent opposée à la largeur. Le mot « oblong » sert à caractériser des objets plus longs que larges. Communément, la longueur d’un objet fait partie de ses dimensions, tout comme la largeur, la hauteur ou encore l’épaisseur, voire comme un diamètre pour un objet de révolution [...]
-
MANDELBROT, Benoît (1924-2010)- Écrit par Olivier GENIN
- 1 média
Benoît Mandelbrot fut un mathématicien franco-américain du 20e-21e siècle. Il est connu pour ses contributions essentielles dans le domaine de la géométrie fractale. Benoît Mandelbrot naît le 20 novembre 1924 à Varsovie (Pologne). Issu d’une famille juive d’origine lituanienne, il doit fuir la Pologne avec sa famille pour échapper aux nazis [...]
-
MILIEUX THÉORÈME DE- Écrit par Olivier GENIN
Le théorème des milieux dit que, dans un triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté. Soit ABC un triangle, soit I le milieu du segment [AB]. Si J est le milieu du segment [AC], alors la droite (IJ) est parallèle à la droite (BC) : La réciproque est vraie : dans un triangle, la droite parallèle à un côté qui passe par le milieu [...]
-
MIRZAKHANI, Maryam (1977-2017)- Écrit par Jean-Claude PICAUD
- 1 média
Maryam Mirzakhani était une mathématicienne iranienne. En 2014, elle a été, à trente-sept ans, la première femme à recevoir la médaille Fields. Cette prestigieuse récompense internationale en mathématiques est décernée, tous les quatre ans, à des chercheurs âgés de moins de quarante ans.Les années d’apprentissage en IranMaryam Mirzakhani naît à Téhéran en 1977, à la veille de la guerre Iran-Irak [...]
-
MORLEY, Frank (1860-1937)- Écrit par Olivier GENIN
Frank Morley fut un mathématicien britannique du 19e et du 20e siècle. Il est surtout connu pour le théorème qui porte son nom. Frank Morley naît le 9 septembre 1860 à Woodbridge, en Angleterre. Il est diplômé de l’université de Cambridge en 1884, puis professeur de mathématiques au collège de Bath jusqu’en 1887, date à laquelle il s’embarque pour les États-Unis, où il se [...]
-
NAPOLÉON THÉORÈME DE- Écrit par Olivier GENIN
- 1 média
Le théorème de Napoléon dit que, si l’on forme 3 triangles équilatéraux à partir des cotés d’un triangle quelconque, alors les centres de gravité de ces 3 triangles (points d’intersection des médianes) forment à leur tour un triangle équilatéral.Construisons un triangle ABC, quelconque, puis extérieurement, 3 triangles équilatéraux ABM, BCP et ACN. Si les points G, H et I désignent les centres de [...]
-
NOMBRE D'OR - Écrit par Olivier GENIN
- 3 médias
Le nombre d’or est égal approximativement à 1,618 033 988 7. Mais, bien plus qu’une valeur, ce chiffre correspond avant tout à une proportion, la « proportion d’or ». Cette proportion est réalisée quand 2 longueurs strictement positives a et b respectent l’égalité suivante :Le nombre d’or est égal à a/b et correspond à l’unique racine positive de l’équation ci-dessus [...]
-
PARALLÈLE - Écrit par Alain MATTHÈS
En géométrie euclidienne, le parallélisme est une propriété relative aux droites. Ainsi, 2 droites dans un plan sont dites parallèles si elles n’ont aucun point commun ou si elles sont confondues. Dans le cas contraire, les droites n’ont qu’un et un seul point commun. Elles sont alors dites sécantes. La géométrie euclidienne a débuté avec les Éléments, ensemble de 13 livres probablement écrits par le mathématicien grec Euclide [...]
-
PAVAGE - Écrit par Olivier GENIN
- 1 média
Paver un plan, c'est recouvrir entièrement ce plan, sans laisser de trou ni faire de superposition, avec une forme de base appelée pavé de base, qu'on reproduit autant qu'on veut en lui faisant subir des transformations simples et répétées. Le pavage peut être géométrique, les formes faisant appel à des polygones simples ou plus ou moins complexes [...]
-
PÉRIMÈTRE ET AIRE - Écrit par Olivier GENIN
- 3 médias
Le périmètre est la mesure de la longueur des contours d’une forme géométrique dans le plan, c'est-à-dire en 2 dimensions, le plus souvent appelées longueur et largeur. L’unité de mesure est le mètre (noté m), avec ses multiples et sous-multiples. L’ aire est la mesure de la surface de la forme géométrique. L’unité de mesure est le mètre carré (noté m2), avec ses multiples et sous-multiples [...]
-
PÉRIMÈTRE - Écrit par Alain MATTHÈS
En géométrie, le périmètre désigne à la fois la longueur du contour d’une surface, mais aussi la ligne qui ferme cette surface. Ce mot est construit à partir du préfixe péri- (« autour ») et du suffixe -mètre (« mesure »). Le périmètre est, avec l’aire, l’une des mesures principales des figures géométriques. Une surface comme un disque est limitée par une ligne, le cercle [...]
-
PERPENDICULAIRE - Écrit par Alain MATTHÈS
En géométrie plane, 2 droites non parallèles sont toujours sécantes (elles se coupent en un point). Elles sont dites perpendiculaires (du latin perpendiculum, « fil à plomb ») lorsqu’elles se coupent en formant un angle droit. Cette définition est aussi valable dans l’espace. On code cette caractéristique par un petit carré à l’intersection des 2 droites [...]
-
PERSPECTIVE - Écrit par Thierry LEMAIRE
- 3 médias
La perspective est un ensemble de règles géométriques permettant de représenter sur une surface plane (bidimensionnelle) des objets en 3 dimensions et de donner ainsi l’illusion de la profondeur. Perspective symbolique Les artistes de l’ Égypte antique ne possèdent pas cette technique de la perspective ; ils se contentent d’une représentation sur un seul plan, et de profil pour les individus [...]
-
PI - Écrit par Olivier GENIN
- 2 médias
Le nombre pi (noté π) est le nombre défini par l’aire du disque ou le périmètre du cercle : – pi est le rapport entre la circonférence du cercle (le périmètre p) et son diamètre D (2 fois le rayon r) :– pi est aussi le rapport entre l’aire du disque (A) et son rayon (r) au carré : La valeur approchée admise de π est 3,141 59 [...]
-
PROJECTION ET RÉFLEXION ,mathématiques - Écrit par Olivier GENIN
- 2 médias
En géométrie, la projection et la réflexion sont 2 transformations qui ne gardent pas les propriétés de la forme initiale déplacée. En cela, elles s’opposent aux déplacements que sont la translation, la rotation, la symétrie axiale et la symétrie centrale. La projection Une projection est une image d’une figure ou d’un objet, projetée sur un support, un plan donné [...]
-
PYTHAGORE (580 env.-500 env. av. J.-C.)- Écrit par Alain MATTHÈS
- 1 média
Le Grec Pythagore fut le premier pur mathématicien. Il serait né vers 580 av. J.-C. dans l’île égéenne de Samos. Il est plus jeune que le philosophe et mathématicien Thalès et les historiens admettent qu’il fut élève de celui-ci. Sa vie, cependant, est obscure et controversée, peu de documents de cette époque étant restés intacts. Pythagore fonde une communauté et vit en son sein [...]
-
PYTHAGORE THÉORÈME DE- Écrit par Olivier GENIN
- 1 média
Le théorème de Pythagore dit que, dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. Dans un triangle rectangle, le côté opposé à l’angle droit est appelé l’hypoténuse. L’hypoténuse est toujours le plus grand des côtés Soit ABC un triangle rectangle en A, alors on a : BC2 = AB2 + AC2 [...]
-
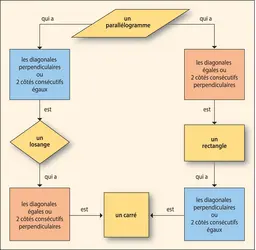
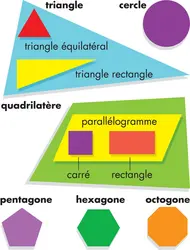
QUADRILATÈRE - Écrit par Alain MATTHÈS
Le quadrilatère est une figure géométrique possédant 4 côtés. Il fait partie de la famille des polygones, figures ayant plusieurs angles. Un quadrilatère noté ABCD possède 4 sommets, qui sont les points A, B, C et D, et 4 côtés, qui sont les segments [AB], [BC], [CD] et [DA]. Il possède aussi 2 diagonales, qui joignent les sommets opposés et sont les segments [AC] et [BD] [...]
-
SYMÉTRIE CENTRALE - Écrit par Olivier GENIN
Une symétrie centrale est une transformation géométrique qui à chaque point associe un point image symétrique par rapport à un centre de symétrie. Si M’ est le symétrique de M par rapport à I alors M est le symétrique de M’ par rapport à I. On dit que M’ et M sont symétriques par rapport à I. Le symétrique de I est I. C’est le seul point dans ce cas [...]
-
SYMÉTRIE - Écrit par Alain MATTHÈS
En mathématiques, la symétrie (du latin symmetria, « justesse des proportions ») est une transformation géométrique qui ne provoque aucune modification de forme ni de dimensions. Dès l’Antiquité, les figures possédant des symétries ont fait l’objet d’intenses études. Le cercle, le triangle équilatéral, le carré et tous les autres polygones réguliers ont révélé d’intéressantes propriétés [...]
-
THALÈS (625 env.-547 env. av. J.-C.)- Écrit par Alain MATTHÈS
- 1 média
Thalès de Milet fut le premier philosophe, scientifique et mathématicien grec. Le monde grec comprenait alors de nombreuses villes dispersées sur le bord des mers Égée et Ionienne. Ces villes étaient reliées aux mondes égyptien et babylonien par bateaux. Les échanges culturels étaient nombreux. Les connaissances mathématiques et astronomiques des uns faisaient souvent le bonheur des autres [...]
-
THALÈS THÉORÈME DE- Écrit par Olivier GENIN
Le théorème de Thalès dit que si (d) et (d’) sont deux droites sécantes en un point A, B et M deux points de la droite (d), distincts de A, C et N deux points de la droite (d’), distincts de A, et si les droites (BC) et (MN) sont parallèles, alors : La figure ABC forme un triangle. D’où l’énoncé restreint du théorème de Thalès, appliqué au triangle [...]
-
TRIANGLE - Écrit par Alain MATTHÈS
Le triangle est une figure géométrique élémentaire formée par 3 points et par les 3 segments qui les relient. Elle fait partie de la famille des polygones et a été nommée à une certaine époque « trigone », c’est à dire figure possédant 3 angles. Les mots « pentagone » et « trigonométrie » ont conservé leur racine grecque gonia, qui signifie « angle » [...]
-
VARIGNON, Pierre (1654-1722)- Écrit par Olivier GENIN
Pierre Varignon fut un mathématicien français du 17e et du 18e siècle. Il est connu pour le théorème qui porte son nom et pour ses travaux en mécanique. Pierre Varignon naît en 1654 à Caen, dans une famille normande modeste. Il étudie la théologie et la philosophie au collège jésuite de Caen et devient prêtre en 1683. Après avoir lu les Éléments d’Euclide, il se [...]
-
VECTEUR ,mathématiques - Écrit par Olivier GENIN
Un vecteur est défini par son origine (ou point de départ), son extrémité (ou point d'arrivée), sa longueur, encore appelée norme du vecteur, sa direction, qui est celle de la droite qui le porte, et son sens, de son origine à son extrémité. Ainsi, le vecteur AB est défini par son origine (le point A), son extrémité (le point B), sa longueur AB, appelée norme et notée [...]
-
VOLUME - Écrit par Alain MATTHÈS
En mathématiques, le volume désigne à la fois la partie de l’espace qu’occupe un objet et sa mesure. Ce terme provient du latin voluminis (« chose enroulée »), formé à partir du verbe volvere, qu’on retrouve dans le mot « révolution ». Les objets de révolution sont obtenus par rotation autour d’un axe, par exemple un cylindre obtenu sur un tour à bois [...]
Documents
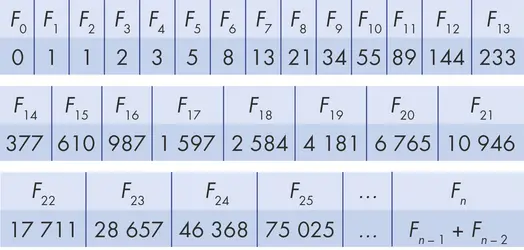
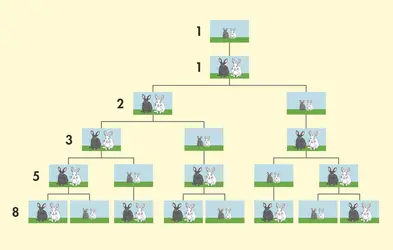
Suite de Leonardo Fibonacci
Fibonacci est à l’origine d’une suite récurrente qui porte son nom. [...]
Les Objets fractals, de Benoît Mandelbrot
Benoît Mandelbrot rassemble dans l’essai Les Objets fractals : forme, hasard et dimension les résultats de ses travaux effectués au centre de recherche Thomas-Watson de la société I.B.M. à… [...]
Le trompe-l’œil
Le trompe-l’œil est une représentation destinée à donner l’illusion de la réalité. Dans sa volonté de « tromper », l’artiste utilise la troisième dimension, une perspective qui fait « sortir » un ou… [...]
Léonard de Vinci et la pespective
Dans son Traité de la peinture, Léonard de Vinci donne des conseils à un apprenti peintre sur la manière de rendre la perspective. [...]
Pythagore et la musique
Pythagore est une figure multiforme et, bien qu’il n’ait laissé aucun écrit, son influence a été considérable. Chef religieux (il avait été initié aux mystères égyptiens), philosophe, mathématicien,… [...]