Nombres et calculs

• Écrit par Alain MATTHÈS

L’addition (du latin addere, « ajouter ») est l’une des 4 opérations élémentaires de l’arithmétique. Elle consiste à compter la réunion d’objets contenus dans des collections. Elle sert aussi à déterminer une grandeur obtenue par l’ajout de 2 grandeurs de même nature, comme les longueurs. Un enfant qui mesurait 147 centimètres et a grandi de 3 centimètres mesure ainsi 150 centimètres [...]

• Écrit par Encyclopædia Universalis

L’arithmétique est la branche la plus élémentaire des mathématiques. C’est elle qui permet de compter et de réaliser les 4 opérations élémentaires (addition, soustraction, multiplication, division). Toutes les autres branches des mathématiques reposent sur ses principes et ses règles. Nous utilisons l’arithmétique tous les jours, pour faire un achat, mesurer une distance ou simplement pour compter [...]

Diophante d'Alexandrie, un mathématicien grec du 3e siècle, parfois appelé le « père de l'algèbre », est connu par son ouvrage les Arithmétiques, qui traite des solutions des équations algébriques. On ne sait pratiquement rien de sa vie, et ses dates de naissance et de mort sont très controversées. Les Arithmétiques sont une collection de solutions numériques de 130 équations [...]

• Écrit par Encyclopædia Universalis
• 1 média

Bien avant l’invention de la calculatrice électronique ou de l’ordinateur, on utilisait un boulier pour compter et calculer. Sur cet instrument, les calculs sont réalisés non pas à l’aide de chiffres, mais de boules. Celles-ci, enfilées sur des tiges disposées dans un cadre, représentent les unités, les dizaines, les centaines, etc. Le boulier a probablement été inventé par un peuple ancien de Mésopotamie (aujourd’hui l’Irak), les Sumériens [...]

• Écrit par Olivier GENIN
• 1 média

On appelle calcul littéral un calcul qui s’effectue avec au moins un nombre dont la valeur est inconnue.Ce nombre est symbolisé par une lettre, souvent x ou y, d’où l’expression « calcul littéral », qui signifie « calcul avec des lettres ».La valeur de ce nombre étant inconnue, il est souvent appelé l’inconnue.Cette technique de calcul, qui « pose une inconnue », permet de résoudre de nombreux problèmes [...]

• Écrit par Olivier GENIN
• 1 média

Le calcul mental, c'est résoudre des calculs « de tête », sans poser d'opération ni utiliser une calculatrice.Deux personnes n’auront pas forcément utilisé les mêmes raccourcis ou chemin de calcul pour trouver le bon résultat d’une opération. Pour résoudre « de tête » un calcul, il faut manier parfaitement « mentalement » les 4 opérations de base : l’addition, la soustraction, la multiplication et la division [...]

• Écrit par Olivier GENIN

La statistique est la science mathématique qui consiste à récolter et à analyser des données chiffrées, afin de les commenter et de pouvoir observer des tendances.Les instituts de sondage sont des organismes qui utilisent la statistique pour décrire, par exemple, l’économie d’un pays, sa démographie, les tendances politiques ou encore la consommation des personnes concernant divers produits [...]

• Écrit par Encyclopædia Universalis
• 1 média

Les chiffres romains sont une manière de représenter les nombres par des lettres de l’alphabet latin. Ce système fut créé il y a environ 2 000 ans, à l’époque de la Rome antique. Il a depuis lors été en grande partie remplacé par les chiffres arabes (1, 2, 3, etc.).Principe de fonctionnementLe système numérique romain utilise 7 lettres comme chiffres : I = 1, V = 5, X = 10, L = 50, C = 100, D = 500 et M = 1 000 [...]

• Écrit par Olivier GENIN
• 2 médias

La comparaison de 2 nombres réels permet de déterminer lequel est le plus grand et lequel est le plus petit. Pour comparer 2 nombres a et b, on les soustrait et on regarde si le résultat est positif, négatif ou nul : Si a - b > 0, alors a est strictement plus grand que b. Si a - b < 0, alors a est strictement plus petit que b [...]

• Écrit par Alain MATTHÈS

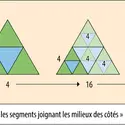
La distributivité (du latin distribuere, « répartir ») est une propriété de la multiplication par rapport à l’addition qui permet de passer d’un produit de sommes à une somme de produits. Une pièce rectangulaire de 13 mètres de longueur et de 5 mètres de largeur a pour superficie 65 mètres carrés, car 13 × 5 = 65. On peut la décomposer en 2 pièces rectangulaires dont l’une a 6 mètres et l’autre 7 mètres de longueur [...]

• Écrit par Alain MATTHÈS

La division (du latin dividere, signifiant « partager ») est l’une des 4 opérations de l’arithmétique élémentaire. Elle permet de partager ou de répartir en plusieurs parties égales. Elle associe à 2 nombres entiers naturels, appelés dividende et diviseur, un entier appelé quotient. Le nombre à diviser est le dividende. Celui qui exprime en combien de parties égales on le divise se nomme diviseur ; ce dernier ne peut jamais être 0 [...]

• Écrit par Alain MATTHÈS

Dans le langage courant, la notion de fonction impose une dépendance entre 2 quantités, par exemple dans l’expression « le prix est fonction de la demande ». En mathématiques, ce mot fut d’abord utilisé comme un mot du langage courant, pour indiquer qu’une quantité dépend d’une autre. Il fallut attendre le 19e siècle pour qu’on en donne une définition précise [...]

• Écrit par Olivier GENIN
• 1 média

Une fraction est une division de 2 nombres entiers relatifs. Son résultat est appelé le quotient : a ∈ (ensemble des nombres entiers relatifs) et b ∈ * (ensemble des entiers relatifs non nuls).Les fractions font parties de la famille des nombres rationnels, notés .La partie au-dessus du trait de fraction, le dividende, est appelée le numérateur [...]

• Écrit par Olivier GENIN

Les identités remarquables permettent de pouvoir factoriser et développer des expressions mathématiques de manière plus simple. Les expressions qui se trouvent à gauche du signe égal (=) sont les produits remarquables : ce sont les formes factorisées. Les expressions qui se trouvent à droite du signe égal sont les sommes remarquables : ce sont les formes développées [...]

• Écrit par Olivier GENIN
• 1 média

Littéralement, le mot « infini » sert à qualifier quelque chose qui est sans limite. Les premières définitions de l’infini furent d’ailleurs des définitions dites négatives. Pour les Grecs et les Romains, « l’infini, c’est tout ce qui n’est pas fini ». Pour Aristote, c’est « ce qui ne se laisse pas parcourir et n’a pas de limite ». Encore aujourd’hui, l’infini est couramment défini comme ce que ce n’est pas [...]

• Écrit par Bernard PIRE
• 1 média

Itérer une opération mathématique, c’est la répéter un certain nombre de fois en prenant le résultat précédent comme point de départ de l’opération suivante. Par exemple, si on itère l’opération « multiplier par 3 » en commençant par le nombre 2, on obtient successivement 6, 18, 54, 162,...Itérer une opération revient souvent à définir une nouvelle opération [...]

• Écrit par Alain MATTHÈS

La multiplication (du latin multiplicatio, qui signifie « augmentation ») est l’une des 4 opérations de l’arithmétique élémentaire. Multiplier un nombre entier par un autre, c’est ajouter cet entier à lui-même plusieurs fois. Lorsque les nombres à ajouter entre eux sont égaux, l’addition prend le nom de multiplication. Ajouter 3 fois un nombre, c’est tripler ce nombre [...]

• Écrit par Olivier GENIN
• 3 médias

Le nombre d’or est égal approximativement à 1,618 033 988 7. Mais, bien plus qu’une valeur, ce chiffre correspond avant tout à une proportion, la « proportion d’or ». Cette proportion est réalisée quand 2 longueurs strictement positives a et b respectent l’égalité suivante :Le nombre d’or est égal à a/b et correspond à l’unique racine positive de l’équation ci-dessus [...]

• Écrit par Alain MATTHÈS

En mathématiques, un nombre décimal s’écrit à l’aide d’une virgule, suivie d’un nombre fini de chiffres. L’existence du zéro en tant que chiffre a permis la création du système décimal, dans lequel un nombre s’écrit à l’aide des 10 chiffres (de 0 à 9) et des groupements qui se font par 10 : la dizaine (10 unités), la centaine (10 dizaines), le millier (10 centaines), etc [...]

• Écrit par Alain MATTHÈS

En mathématiques, un nombre entier relatif se compose d’un entier naturel précédé d’un signe positif (+) ou négatif (-). Les entiers positifs s’identifient aux entiers naturels (1, 2, 3, etc.), tandis que les entiers négatifs sont leurs opposés (- 1, - 2, - 3, etc.). Le chiffre 0 fait aussi partie des nombres entiers relatifs, mais il est dépourvu de signe [...]

• Écrit par Alain MATTHÈS

En mathématiques, un nombre entier est un nombre naturel positif (1, 2, 3, etc.) ou un nombre nul (0) permettant de compter des objets distincts. L’étude des entiers, avec notamment les opérations d’addition et de multiplication, constitue une branche élémentaire des mathématiques appelée arithmétique. Les nombres sont écrits à l’aide de chiffres. De nombreuses civilisations (notamment [...]

• Écrit par Encyclopædia Universalis
• 3 médias

Un nombre est un concept de base en mathématique, servant à compter, à mesurer et à comparer des quantités. Un système de notation numérale est un ensemble de symboles représentant des nombres. Le système de notation numérale le plus courant recourt à 10 symboles, les chiffres (0, 1, 2, 3, 4, 5, 6, 7, 8, et 9), utilisés seuls ou en combinaisons. Types de nombres Les nombres peuvent être classés de plusieurs manières [...]

• Écrit par Olivier GENIN

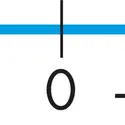
Souvent, les notions d’inverse et d’opposé en mathématiques prêtent à confusion.Deux nombres réels opposés sont 2 nombres qui ont la même partie numérique, mais des signes différents. Leurs distances par rapport à l’origine O d’un axe sont égales, mais opposées. Ainsi, sur un axe horizontal gradué, zéro est au centre du segment [– aa] formé par 2 nombres opposés [...]

• Écrit par Olivier GENIN
• 1 média

Un nombre parfait est un nombre entier naturel dont la somme des diviseurs propres (diviseurs différents du nombre lui-même) est égale à ce nombre. Par exemple, 6 est divisible par 1, 2 et 3, et 6 = 1 + 2 + 3.Dès l’Antiquité, au 3e siècle av. J.-C., Euclide expérimentait les nombres parfaits. Au 17e siècle, Euler reprend les travaux d’Euclide et prouve une formule pour les nombres parfaits pairs [...]

• Écrit par Olivier GENIN
• 1 média

Un nombre premier est un nombre entier supérieur ou égal à 2 et divisible uniquement par 1 et par lui-même pour donner un nombre entier : 2 est le seul nombre premier pair. Il existe une infinité de nombres premiers, qui sont donc tous impairs.L’étude des nombres premiers fait partie de la branche des mathématiques appelée l’arithmétique.C’est le mathématicien grec Euclide qui, au 3e siècle av [...]

• Écrit par Olivier GENIN

Les 4 opérations mathématiques élémentaires sont l’addition, la soustraction, la multiplication et la division. Les symboles respectifs sont +, –, × et : ; ils sont appelés opérateurs. Les chiffres ou les variables qu’ils font intervenir sont appelés opérandes. La mise à la puissance d’un opérande est aussi une opération mathématique.Addition et soustraction Pour effectuer une suite d’additions [...]

• Écrit par Olivier GENIN
• 1 média

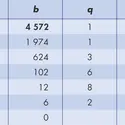
Le PGCD et le PPCM sont, respectivement, le plus grand commun diviseur et le plus petit commun multiple entre 2 nombres entiers naturels.Le PGCDLe PGCD de 2 nombres entiers naturels a et b (a, b ∈ ) correspond donc au plus grand nombre k qui divise à la fois a et b :etLe PGCD permet notamment de simplifier les fractions complexes [...]

• Écrit par Olivier GENIN
• 2 médias

Le nombre pi (noté π) est le nombre défini par l’aire du disque ou le périmètre du cercle : – pi est le rapport entre la circonférence du cercle (le périmètre p) et son diamètre D (2 fois le rayon r) :– pi est aussi le rapport entre l’aire du disque (A) et son rayon (r) au carré : La valeur approchée admise de π est 3,141 59 [...]

• Écrit par Alain MATTHÈS

Un pourcentage est un rapport entre 2 nombres qui s’exprime sous la forme d’une fraction dont le dénominateur est 100. Pour mesurer l’importance d’une partie quantifiable ayant une caractéristique particulière par rapport à un ensemble auquel elle appartient, on utilise un rapport. Par exemple, si dans 20 centilitres d’une boisson il y a 5 centilitres de jus d’orange, alors un quart (5/20) de cette boisson est constituée de jus d’orange [...]

• Écrit par Olivier GENIN
• 1 média

La puissance n-ième d’un nombre a est : (a est multiplié par lui-même n fois, on a donc n facteurs). an se dit « a puissance n » ou « a exposant n ».L’exposant n est un nombre entier non nul.Un nombre à l’exposant 1 ne change pas le nombre :Un nombre à l’exposant 0 est toujours [...]

• Écrit par Bernard PIRE
• 1 média

Le mot puissance est employé dans divers domaines scientifiques, avec des sens différents. La puissance en physique En physique, la puissance d’une machine est la quantité d’énergie qu’elle peut fournir ou consommer pendant 1 seconde. On la mesure généralement en watt (W), du nom du physicien écossais James Watt qui a tellement amélioré les machines à vapeur qu’on considère que ses travaux furent essentiels pour la révolution industrielle [...]

• Écrit par Olivier GENIN
• 1 média

La racine carrée d’un nombre strictement positif a est le nombre positif, noté , qui, élevé au carré, donne a : La racine carrée d’un nombre au carré, est égale à ce nombre : La racine carrée d’un nombre négatif n’existe pas : .En revanche, et existent.Le produit de 2 racines carrées est égal à la racine carrée du produit :Le quotient de 2 racines carrées est égal à la racine [...]

• Écrit par Alain MATTHÈS

La règle de trois est une méthode de calcul qui fait intervenir 3 valeurs pour en obtenir une quatrième. Les 3 nombres a, b et c étant donnés, il s’agit de déterminer un nombre d tel que a et b soient proportionnels à c et d. On appelle quatrième proportionnelle le quatrième nombre d [...]

• Écrit par Alain MATTHÈS

La soustraction (du latin substractio, qui signifie l’« action de se retirer ») est une des 4 opérations élémentaires de l’arithmétique. Elle consiste à retrancher un nombre d’un autre. On considère parfois que la soustraction est l’opposé de l’addition. Celle-ci consiste en effet à enlever un nombre au lieu de l’ajouter. Quand on veut ôter un nombre d’un autre, la première idée est de [...]

• Écrit par Olivier GENIN
• 1 média

La notion de zéro, comme la notion d’infini, est difficile à cerner et à définir pour l’homme. Philosophiquement, le zéro est lié au néant, au vide. En théologie, zéro serait le moment juste avant la naissance de notre Univers. En physique, ce serait l’instant exact du big bang. En mathématiques, le zéro a été créé par nécessité, notamment pour des besoins de calculs arithmétiques [...]