médiatrice, géométrie

Articles associés

• CERCLE CIRCONSCRIT

  • Écrit par Olivier GENIN
  • 3 médias
  

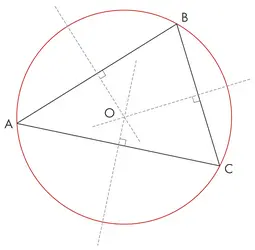
  Un cercle circonscrit à un polygone est un cercle qui, s’il existe, passe par tous les sommets de ce polygone. À l’inverse, un cercle inscrit dans un polygone est un cercle qui, s’il existe, est tangent à chaque côté du polygone. On ne s’intéresse ici qu’au cas du cercle circonscrit à un triangle rectangle. Soit un cercle c de centre O et [BC] un diamètre du cercle [...]

• DÉPLACEMENTS, mathématiques

  • Écrit par Olivier GENIN

  En géométrie, un déplacement est une transformation qui garde les propriétés de la forme initiale déplacée. Un déplacement conserve les formes (une droite donne une droite, un carré donne un carré, etc.). Il conserve les mesures (longueurs, angles, aires). Il conserve les propriétés géométriques des figures (conservation des parallèles et des perpendiculaires, etc [...]

• DROITES REMARQUABLES DANS LE TRIANGLE

  • Écrit par Olivier GENIN

  Une droite est dite remarquable dans un triangle lorsqu’elle possède une ou plusieurs propriétés quel que soit le triangle. Il existe 4 types de droites remarquables dans le triangle : la médiane, la médiatrice, la hauteur et la bissectrice. Médianes dans le triangle La médiane est la droite qui passe par le milieu d’un côté du triangle et par le sommet opposé à ce côté [...]

• PERPENDICULAIRE

  • Écrit par Alain MATTHÈS

  En géométrie plane, 2 droites non parallèles sont toujours sécantes (elles se coupent en un point). Elles sont dites perpendiculaires (du latin perpendiculum, « fil à plomb ») lorsqu’elles se coupent en formant un angle droit. Cette définition est aussi valable dans l’espace. On code cette caractéristique par un petit carré à l’intersection des 2 droites [...]

• SYMÉTRIE

  • Écrit par Alain MATTHÈS

  En mathématiques, la symétrie (du latin symmetria, « justesse des proportions ») est une transformation géométrique qui ne provoque aucune modification de forme ni de dimensions. Dès l’Antiquité, les figures possédant des symétries ont fait l’objet d’intenses études. Le cercle, le triangle équilatéral, le carré et tous les autres polygones réguliers ont révélé d’intéressantes propriétés [...]

Médias