triangle

Article principal

• TRIANGLE

  • Écrit par Alain MATTHÈS

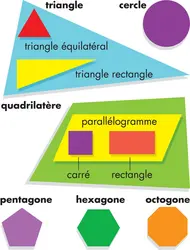
  Le triangle est une figure géométrique élémentaire formée par 3 points et par les 3 segments qui les relient. Elle fait partie de la famille des polygones et a été nommée à une certaine époque « trigone », c’est à dire figure possédant 3 angles. Les mots « pentagone » et « trigonométrie » ont conservé leur racine grecque gonia, qui signifie « angle » [...]

Articles associés

• AIRE

  • Écrit par Alain MATTHÈS

  En géométrie, l’aire (du latin area, qui signifie « surface plane ») désigne la mesure d’une surface. En géographie, le terme « superficie » lui est préféré. Dans la langue de tous les jours, si une « surface » peut être cultivée, c’est la « superficie » cultivée qui est exprimée en hectares. Les Égyptiens savaient déjà évaluer les aires des figures planes comme le triangle, le rectangle ou le trapèze [...]

• DROITES REMARQUABLES DANS LE TRIANGLE

  • Écrit par Olivier GENIN

  Une droite est dite remarquable dans un triangle lorsqu’elle possède une ou plusieurs propriétés quel que soit le triangle. Il existe 4 types de droites remarquables dans le triangle : la médiane, la médiatrice, la hauteur et la bissectrice. Médianes dans le triangle La médiane est la droite qui passe par le milieu d’un côté du triangle et par le sommet opposé à ce côté [...]

• GÉOMÉTRIE

  • Écrit par Encyclopædia Universalis
  • 3 médias
  

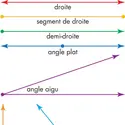
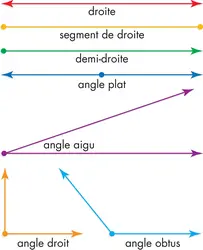
  La géométrie est une science mathématique qui étudie les formes et les figures. Elle explique comment construire ou dessiner, mesurer et comparer des formes. On utilise notamment la géométrie pour bâtir des maisons et des ponts, mais aussi pour organiser des voyages dans l’espace. Points, droites et angles La géométrie repose sur les notions de point, de droite et d’angle [...]

• HOMOTHÉTIE

  • Écrit par Olivier GENIN

  Une homothétie est la transformation de centre O et de rapport k qui à tout point M associe le point M’ tel que : OM’ = kOM .La notation est : hO,k(M) = M’ ou hO,k : M → M’. M’ est l’image de M, et k est le rapport, c’est-à-dire la proportion entre le vecteur final et le vecteur initial [...]

• MILIEUX THÉORÈME DE

  • Écrit par Olivier GENIN

  Le théorème des milieux dit que, dans un triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté. Soit ABC un triangle, soit I le milieu du segment [AB]. Si J est le milieu du segment [AC], alors la droite (IJ) est parallèle à la droite (BC) : La réciproque est vraie : dans un triangle, la droite parallèle à un côté qui passe par le milieu [...]

• MORLEY, Frank (1860-1937)

  • Écrit par Olivier GENIN

  Frank Morley fut un mathématicien britannique du 19e et du 20e siècle. Il est surtout connu pour le théorème qui porte son nom. Frank Morley naît le 9 septembre 1860 à Woodbridge, en Angleterre. Il est diplômé de l’université de Cambridge en 1884, puis professeur de mathématiques au collège de Bath jusqu’en 1887, date à laquelle il s’embarque pour les États-Unis, où il se [...]

• NAPOLÉON THÉORÈME DE

  • Écrit par Olivier GENIN
  • 1 média
  

  Le théorème de Napoléon dit que, si l’on forme 3 triangles équilatéraux à partir des cotés d’un triangle quelconque, alors les centres de gravité de ces 3 triangles (points d’intersection des médianes) forment à leur tour un triangle équilatéral.Construisons un triangle ABC, quelconque, puis extérieurement, 3 triangles équilatéraux ABM, BCP et ACN. Si les points G, H et I désignent les centres de [...]

• PÉRIMÈTRE ET AIRE

  • Écrit par Olivier GENIN
  • 3 médias
  

  Le périmètre est la mesure de la longueur des contours d’une forme géométrique dans le plan, c'est-à-dire en 2 dimensions, le plus souvent appelées longueur et largeur. L’unité de mesure est le mètre (noté m), avec ses multiples et sous-multiples. L’aire est la mesure de la surface de la forme géométrique. L’unité de mesure est le mètre carré (noté m2), avec ses multiples et sous-multiples [...]

• SYMÉTRIE CENTRALE

  • Écrit par Olivier GENIN

  Une symétrie centrale est une transformation géométrique qui à chaque point associe un point image symétrique par rapport à un centre de symétrie. Si M’ est le symétrique de M par rapport à I alors M est le symétrique de M’ par rapport à I. On dit que M’ et M sont symétriques par rapport à I. Le symétrique de I est I. C’est le seul point dans ce cas [...]

• THALÈS THÉORÈME DE

  • Écrit par Olivier GENIN

  Le théorème de Thalès dit que si (d) et (d’) sont deux droites sécantes en un point A, B et M deux points de la droite (d), distincts de A, C et N deux points de la droite (d’), distincts de A, et si les droites (BC) et (MN) sont parallèles, alors : La figure ABC forme un triangle. D’où l’énoncé restreint du théorème de Thalès, appliqué au triangle [...]

• TRIGONOMÉTRIE DANS LE TRIANGLE RECTANGLE

  • Écrit par Olivier GENIN
  • 1 média
  

  La trigonométrie étudie les relations existant entre les longueurs des côtés d’un triangle et les mesures de ses angles. La trigonométrie est utilisée depuis longtemps en astronomie, en géographie, et par les marins. L’hypoténuse est le coté opposé à l’angle droit. C’est toujours le plus grand des côtés dans un triangle rectangle.Le côté opposé et le côté adjacent sont les deux côtés de l’angle [...]

Médias