droite, géométrie

Articles associés

• COMPARAISON, mathématiques

  • Écrit par Olivier GENIN
  • 2 médias
  

  La comparaison de 2 nombres réels permet de déterminer lequel est le plus grand et lequel est le plus petit. Pour comparer 2 nombres a et b, on les soustrait et on regarde si le résultat est positif, négatif ou nul : Si a - b > 0, alors a est strictement plus grand que b. Si a - b < 0, alors a est strictement plus petit que b [...]

• DROITE ÉQUATION DE

  • Écrit par Olivier GENIN

  Une droite est un ensemble illimité de points. Pour la représenter géométriquement, il faut définir un repère, connaître les coordonnées d’au moins 2 de ses points ou son équation. Le repère Dans le plan, un repère a 2 axes, qu'on appelle axe des abscisses pour l’axe horizontal et axe des ordonnées pour l’axe vertical. Le point d'intersection est l'origine du repère et se note généralement O [...]

• DROITES REMARQUABLES DANS LE TRIANGLE

  • Écrit par Olivier GENIN

  Une droite est dite remarquable dans un triangle lorsqu’elle possède une ou plusieurs propriétés quel que soit le triangle. Il existe 4 types de droites remarquables dans le triangle : la médiane, la médiatrice, la hauteur et la bissectrice. Médianes dans le triangle La médiane est la droite qui passe par le milieu d’un côté du triangle et par le sommet opposé à ce côté [...]

• GÉOMÉTRIE

  • Écrit par Encyclopædia Universalis
  • 3 médias
  

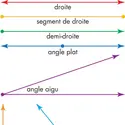
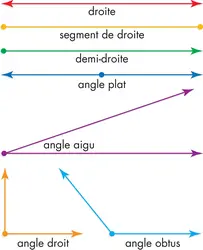
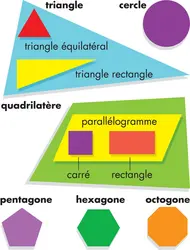
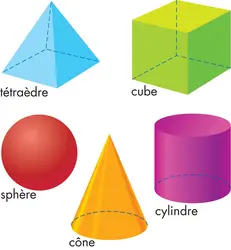
  La géométrie est une science mathématique qui étudie les formes et les figures. Elle explique comment construire ou dessiner, mesurer et comparer des formes. On utilise notamment la géométrie pour bâtir des maisons et des ponts, mais aussi pour organiser des voyages dans l’espace. Points, droites et angles La géométrie repose sur les notions de point, de droite et d’angle [...]

• INFINI, mathématiques

  • Écrit par Olivier GENIN
  • 1 média
  

  Littéralement, le mot « infini » sert à qualifier quelque chose qui est sans limite. Les premières définitions de l’infini furent d’ailleurs des définitions dites négatives. Pour les Grecs et les Romains, « l’infini, c’est tout ce qui n’est pas fini ». Pour Aristote, c’est « ce qui ne se laisse pas parcourir et n’a pas de limite ». Encore aujourd’hui, l’infini est couramment défini comme ce que ce n’est pas [...]

• PARALLÈLE

  • Écrit par Alain MATTHÈS

  En géométrie euclidienne, le parallélisme est une propriété relative aux droites. Ainsi, 2 droites dans un plan sont dites parallèles si elles n’ont aucun point commun ou si elles sont confondues. Dans le cas contraire, les droites n’ont qu’un et un seul point commun. Elles sont alors dites sécantes. La géométrie euclidienne a débuté avec les Éléments, ensemble de 13 livres probablement écrits par le mathématicien grec Euclide [...]

• PERPENDICULAIRE

  • Écrit par Alain MATTHÈS

  En géométrie plane, 2 droites non parallèles sont toujours sécantes (elles se coupent en un point). Elles sont dites perpendiculaires (du latin perpendiculum, « fil à plomb ») lorsqu’elles se coupent en formant un angle droit. Cette définition est aussi valable dans l’espace. On code cette caractéristique par un petit carré à l’intersection des 2 droites [...]

• SYMÉTRIE

  • Écrit par Alain MATTHÈS

  En mathématiques, la symétrie (du latin symmetria, « justesse des proportions ») est une transformation géométrique qui ne provoque aucune modification de forme ni de dimensions. Dès l’Antiquité, les figures possédant des symétries ont fait l’objet d’intenses études. Le cercle, le triangle équilatéral, le carré et tous les autres polygones réguliers ont révélé d’intéressantes propriétés [...]

Médias