GÉOMÉTRIE

La géométrie est une science mathématique qui étudie les formes et les figures. Elle explique comment construire ou dessiner, mesurer et comparer[...]

Points, droites et angles

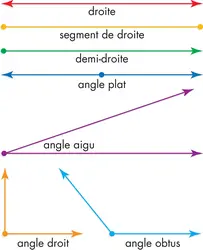
La géométrie repose sur les notions de point, de droite et d’angle. Un point est un objet qui n’a ni longueur ni largeur. Une droite est un objet qui s’étend à l’infini dans les 2 sens. Un segment de droite est une portion de droite comprise entre 2 points. Une demi-droite est une partie de droite, ayant un point pour extrémité.

Deux demi-droites qui partagent la même extrémité forment un angle. Si les demi-droites[...]

Polygones

Un polygone est une figure fermée formée par plusieurs segments de droite réunis. Un polygone à 3 côtés est un triangle. Certains triangles portent des noms spéciaux. Si les 3 côtés d’un triangle sont égaux, le triangle est équilatéral. Un triangle qui a 2 côtés de même longueur est un triangle isocèle. Un triangle dont l’un des angles est droit est un triangle rectangle.

Un polygone à 4 côtés est[...]

Cercles

Certaines formes géométriques sont composées de courbes et non de droites. Le cercle est la plus connue. Tous les points appartenant au cercle sont à la même distance du centre. Cette distance s’appelle le rayon.[...]

Solides

Les triangles, les carrés et les cercles sont des formes planes. D’autres formes géométriques sont des solides. Un cube (boîte carrée par exemple) est un solide composé de surfaces planes.[...]