Napoléon, théorème de
Le théorème de Napoléon dit que, si l’on forme 3 triangles équilatéraux à partir des cotés d’un triangle quelconque, alors les centres de gravité de ces 3 triangles (points d’intersection des médianes) forment à leur tour un triangle équilatéral.
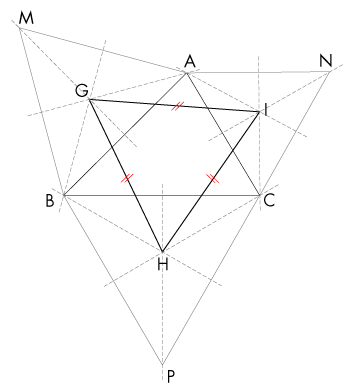
Construisons un triangle ABC, quelconque, puis extérieurement, 3 triangles équilatéraux ABM, BCP et ACN. Si les points G, H et I désignent les centres de gravité respectifs des 3 triangles, points d’intersections des médianes de chaque triangle, alors GHI est un triangle équilatéral.
Ce théorème est vrai aussi si les 3 triangles équilatéraux sont tracés à l’intérieur du triangle quelconque.
On attribue ce théorème à Napoléon Ier, mais sans aucune certitude. Il l’aurait trouvé en 1787. Ce qui est certain, c’est que [...]
La suite de cet article est accessible aux abonnés
- Des contenus adaptés au niveau Junior
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
« Napoléon, théorème de » est également traité dans :
droites remarquables dans le triangle
Une droite est dite remarquable dans un triangle lorsqu’elle possède une ou plusieurs propriétés quel que soit le triangle. Il existe 4 types de droites remarquables dans le triangle : la médiane, la médiatrice, la h... Lire l’article
triangle
Le triangle est une figure géométrique élémentaire formée par 3 points et par les 3 segments qui les relient. Elle fait partie de la famille des polygones et a été nommée à une certaine époque « trigone », c’est à di... Lire l’article
