Cercle circonscrit
© Encyclopædia Universalis France
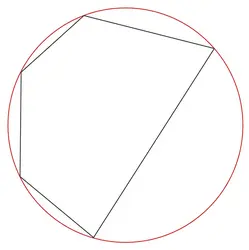
Un cercle circonscrit à un polygone est un cercle qui, s’il existe, passe par tous les sommets de ce polygone. À l’inverse, un cercle inscrit dans un polygone est un cercle qui, s’il existe, est tangent à chaque côté du polygone.
On ne s’intéresse ici qu’au cas du cercle circonscrit à un triangle rectangle.
Soit un cercle cde centre O et[BC]un diamètre du cercle.
Soit un point A quelconque sur le périmètre du cercle.
Alors le triangle ABC est un triangle rectangle, quel que soit le point A choisi.
Le diamètre BC est l’ hypoténuse du triangle rectangle ABC.
Les points A, B, C sont tous sur le cercle c, qui est le cercle circonscrit au triangle ABC rectangle en A.
Le centre du cercle circonscrit, le point O, est le milieu de l’hypoténuse BC.
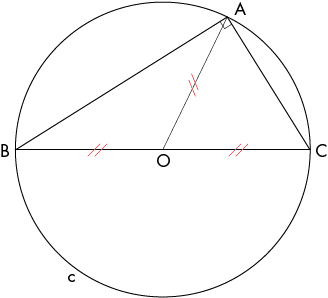
La médiane OA est un rayon r du cercle circonscrit et :
[OA]=[OB]=[OC]= r
.D’une manière générale, le centre du cercle[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
