hypoténuse

Articles associés

• CERCLE CIRCONSCRIT

  • Écrit par Olivier GENIN
  • 3 médias
  

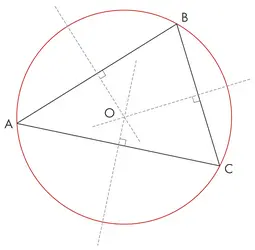
  Un cercle circonscrit à un polygone est un cercle qui, s’il existe, passe par tous les sommets de ce polygone. À l’inverse, un cercle inscrit dans un polygone est un cercle qui, s’il existe, est tangent à chaque côté du polygone. On ne s’intéresse ici qu’au cas du cercle circonscrit à un triangle rectangle. Soit un cercle c de centre O et [BC] un diamètre du cercle [...]

• PYTHAGORE THÉORÈME DE

  • Écrit par Olivier GENIN
  • 1 média
  

  Le théorème de Pythagore dit que, dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. Dans un triangle rectangle, le côté opposé à l’angle droit est appelé l’hypoténuse. L’hypoténuse est toujours le plus grand des côtés Soit ABC un triangle rectangle en A, alors on a : BC2 = AB2 + AC2 [...]

• TRIGONOMÉTRIE DANS LE TRIANGLE RECTANGLE

  • Écrit par Olivier GENIN
  • 1 média
  

  La trigonométrie étudie les relations existant entre les longueurs des côtés d’un triangle et les mesures de ses angles. La trigonométrie est utilisée depuis longtemps en astronomie, en géographie, et par les marins. L’hypoténuse est le coté opposé à l’angle droit. C’est toujours le plus grand des côtés dans un triangle rectangle.Le côté opposé et le côté adjacent sont les deux côtés de l’angle [...]

Médias