Mathématiques
© Glow Images/ Getty Images
Les mathématiques étudient les nombres ainsi que leurs relations entre eux et avec le monde réel. Elles sont souvent décrites[...]
Types de mathématiques
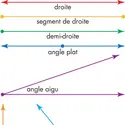
Les mathématiques comprennent plusieurs branches, dont l’arithmétique, l’algèbre, la géométrie, la trigonométrie, le calcul, les statistiques et les probabilités.
Les mathématiques peuvent être pures ou appliquées. Les mathématiques pures étudient les mathématiques[...]
Histoire
On utilise les mathématiques depuis très longtemps. Les Égyptiens se servirent de l’arithmétique et de la géométrie pour construire les pyramides. Les Babyloniens de l’ancienne Mésopotamie (aujourd’hui en Irak) inventèrent un système numérique complexe et utilisaient des fractions.
Les Grecs de l’Antiquité firent beaucoup progresser les mathématiques. Vers 300 av. J.-C., Euclide écrivit notamment un livre important sur la géométrie, Les Éléments. La contribution des Arabes fut aussi essentielle. Vers 800 apr. J.-C., al-Khuwarizmi décrivit ainsi un système de résolution des problèmes, l’algèbre.[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
