La preuve par 3
© 2014 Encyclopædia Universalis
La preuve est un argument qui convainc une personne dès lors que celle-ci le comprend. On prouve pour établir la vérité, qu’elle soit judiciaire ou scientifique. L’énoncé d’un théorème mathématique sera prouvé si les élèves sont convaincus de sa vérité par la justification que le professeur en donne, par exemple par une démonstration logique ou une construction géométrique.
En dehors du domaine des mathématiques, il est difficile de prouver qu’une affirmation scientifique est juste. Quand on essaie de prouver expérimentalement une affirmation (par exemple que l’eau gèle à 0 0C), le résultat mesuré peut au mieux indiquer qu’il ne contredit pas l’affirmation. Mais, comme toute mesure, le résultat est accompagné d’une incertitude, et cela car aucun instrument n’est parfait. Une bonne mesure ne constitue donc pas une preuve définitive. De fait, le perfectionnement des instruments amène souvent à faire évoluer une théorie scientifique.
On peut en revanche à coup sûr prouver qu’une théorie scientifique est fausse en établissant un résultat expérimental contraire à ses prévisions. Ainsi Louis Pasteur démontra que la théorie de la génération spontanée des micro-organismes vivants dans la matière était fausse. : il multiplia les expériences avec des ballons stériles pour montrer qu’une contamination était indispensable à l’apparition des microbes.
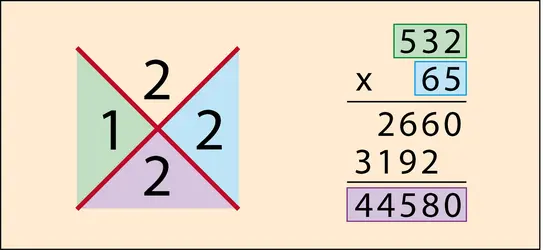
Attention ! Ce qu’on appelle la « preuve par 9 » pour vérifier le résultat d’une multiplication n’est en fait pas vraiment[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
